Cho hàm số \(f\left( x \right)=\,{{x}^{4}}+2{{x}^{2}}+1\). Có bao nhiêu giá trị nguyên của tham số \(m\in \left[ 0\,;\,10 \right]\) để hàm số \(g\left( x \right)=f\left( 3\left| x-m \right|+{{m}^{2}} \right)\) nghịch biến trên \(\left( -\infty \,;\,1 \right)\)?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXét hàm số \(f\left( x \right)=\,{{x}^{4}}+2{{x}^{2}}+1\)
Ta có \({f}'\left( x \right)=4{{x}^{3}}+4x\); \({f}'\left( x \right)=0\Leftrightarrow x=0\)
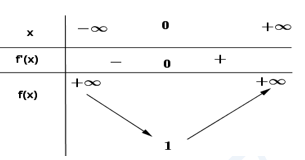
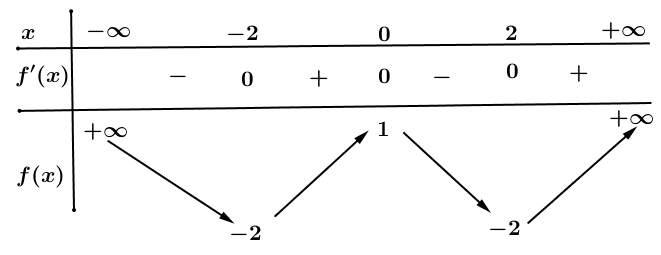
Bảng biến thiên
Ta có \({g}'\left( x \right)={f}'\left( 3\left| x-m \right|+{{m}^{2}} \right).{{\left( 3\left| x-m \right|+{{m}^{2}} \right)}^{\prime }}\) =\({f}'\left( 3\left| x-m \right|+{{m}^{2}} \right).\frac{3\left( x-m \right)}{\left| x-m \right|}\).
\({g}'\left( x \right)=0\) \(\Leftrightarrow \left[ \begin{align} & x-m=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \\ & 3\left| x-m \right|+{{m}^{2}}=0\,\,\,\left( 2 \right) \\ \end{align} \right.\)
TH1: Nếu \(m=0\) \(\Rightarrow \) phương trình \({g}'\left( x \right)=0\Leftrightarrow x=0\)\(\Rightarrow \) không thỏa mãn nghịch biến trên khoảng \(\left( -\infty \,;\,1 \right)\) nên trường hợp này bị loại.
TH2: Nếu \(m>0\) \(\Rightarrow \) phương trình \({g}'\left( x \right)=0\Leftrightarrow x=m\)
Ta có \(3\left| x-m \right|+{{m}^{2}}>0\,\,\forall x<1\)\(\Rightarrow {f}'\left( 3\left| x-m \right|+{{m}^{2}} \right)>0\,\,\forall \,x\in \left( -\infty \,;\,1 \right)\) nên \({g}'\left( x \right) < 0\)\( \Leftrightarrow x < m\).
\(\Rightarrow \) hàm số \(y=g\left( x \right)\) nghịch biến trên \(\left( -\infty \,;\,1 \right)\)\(\Leftrightarrow {g}'\left( x \right)<0\,\forall \,x\in \left( -\infty \,;\,1 \right)\)
\(\Leftrightarrow \,\left( -\infty \,;\,1 \right)\subset \left( -\infty \,;\,m \right)\Leftrightarrow 1\le m\)\(\Rightarrow m\in \left\{ 1;2;3;4\,;5;6;7;8;9;10 \right\}\). Nên có 10 giá trị thỏa mãn.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Lê Quý Đôn
.png)











