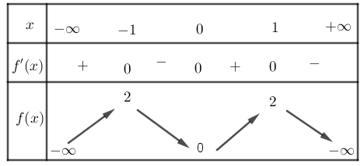
Cho hàm số \(y=\,f(x)=\,a{{x}^{3}}+b{{x}^{2}}+cx+d,\,\)\((a,\,b,\,c,\,d\,\in \mathbb{R},\,a\ne \,0)\). Biết đồ thị \((C)\) của hàm số \(y=\,f(x)\) tiếp xúc với trục hoành tại điểm có hoành độ âm. Đồ thị hàm số \(y=\,{f}'(x)\) như hình vẽ.

Tính diện tích \(S\) của hình phẳng tạo bởi đồ thị \((C)\) và trục hoành.

Câu hỏi liên quan

• Trong không gian \(Oxyz\), cho đường thẳng \(d:\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z+3}{2}\). Trong các vectơ sau, vectơ nào là vectơ chỉ phương của đường thẳng \(d\)?

• :Trong mặt phẳng tọa độ \(O\,xy,\,\) tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(3+\overline{iz}\) là số thuần ảo, là một đường thẳng có phương trình:

• Cho hai tích phân \({\int\limits_{2}^{5}{f\left( x \right)\text{d}x}=8}\) và\({\int\limits_{2}^{5}{g\left( x \right)\text{d}x}=3}\). Tính\({I=\int\limits_{2}^{5}{\left[ f\left( x \right)-g\left( x \right) \right]\text{d}x}}\)?

ZUNIA12

• Cho hàm số \(y=\frac{x+a}{bx+c}\) có đồ thị như hình dưới.

  

  Khẳng định nào sau đây là đúng?

• Cho hàm số \(f\left( x \right)\) liên tục trên tập \(\mathbb{R}\) thỏa mãn \(\int\limits_{0}^{1}{f\left( 2x \right)\text{d}x}=-5\). Tính tích phân \(I=\int\limits_{0}^{2}{f\left( x \right)\text{d}x}\)

• Có bao nhiêu cặp số nguyên dương \(\left( x;y \right)\) thỏa mãn điều kiện \(x\le 2022\) và \(3\left( {{9}^{y}}+2y \right)+2\le x+{{\log }_{3}}{{\left( x+1 \right)}^{3}}\)?

• Số giá trị nguyên nhỏ hơn \(2020\) của tham số \(m\) để phương trình\({{{\log }_{6}}\left( 2020x+m \right)={{\log }_{4}}\left( 1010x \right)}\) có nghiệm là

• Tính đạo hàm của hàm số \(y={{3}^{2x+1}}.\)

• Xét các số phức \(w,{{z}_{1}},{{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}}+1+2i \right|+\left| {{z}_{1}}-5-6i \right|=10\) và \(\left| w+i \right|=\frac{3\sqrt{5}}{5}\), \(5w=\left( 2+i \right)\left( {{z}_{2}}-4 \right)\). Gọi \(a\) là giá trị nhỏ nhất của biểu thức \(P=\left| {{z}_{1}}+{{z}_{2}} \right|\). Khẳng định nào sau đây đúng?

• Một cấp số cộng \(\left( {{u}_{n}} \right)\) có \({{u}_{13}}=8\) và công sai \(d=-3.\) Tìm số hạng thứ ba của cấp số cộng \(\left( {{u}_{n}} \right).\)

• Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau

  

  Số nghiệm thuộc khoảng \(\left( -\infty ;\ln 2 \right)\) của phương trình \(2020f\left( 1-{{e}^{x}} \right)-2021=0\) là

• Cho hàm số \(y=f(x)\) có đạo hàm \({f}'(x)=(2-x){{\left( {{x}^{3}}-{{x}^{2}}-m \right)}^{2021}},\forall x\in \mathbb{R}\). Có bao nhiêu giá trị nguyên thuộc khoảng \((-2021 ; 2022)\) của tham số \(\mathrm{m}\) để hàm số \(g(x)=f\left(x^{2}-2\right)+\frac{1}{2} x^{4}-4 x^{2}+2022\) có đúng 5 điểm cực trị?

• Cho tập hợp \(A\) có \(7\) phần tử. Số tập con có \(3\) phần tử của tập \(A\) là

• Cho hàm số \(f\left( x \right)=\,{{x}^{4}}+2{{x}^{2}}+1\). Có bao nhiêu giá trị nguyên của tham số \(m\in \left[ 0\,;\,10 \right]\) để hàm số \(g\left( x \right)=f\left( 3\left| x-m \right|+{{m}^{2}} \right)\) nghịch biến trên \(\left( -\infty \,;\,1 \right)\)?

• Trong không gian với hệ toạ độ \(Oxyz\), cho điểm \(M\left( 2;-3;1 \right)\) và mặt phẳng \(\left( \alpha  \right):x+3y-z+2=0\). Đường thẳng \(d\) đi qua điểm \(M\) và vuông góc với mặt phẳng \(\left( \alpha  \right)\) có phương trình là

• Tập xác định của hàm số \(y={{\left( {{x}^{2}}-x-2 \right)}^{-10}}\) là

• Số nghiệm thực phân biệt của phương trình \({{5}^{{{x}^{2}}}}{{3}^{{{x}^{2}}+1}}=1\) là

• Trong không gian cho mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-4 \right)}^{2}}=9\). Từ điểm \(A\left( 4;0;1 \right)\)nằm ngoài mặt cầu kẻ một tiếp tuyến bất kỳ đến \(\left( S \right)\) với tiếp điểm \(M\). Tập hợp tất cả các điểm \(M\) là đường tròn có bán kính bằng

• Cho hàm số \(f\left( x \right)\) thỏa mãn \(f'\left( x \right)=\left( 2x+1 \right){{e}^{x-f\left( x \right)}}\) với mọi \(x\in \left( \frac{1}{2};+\infty  \right)\) và \(f\left( 1 \right)=1\). Có bao nhiêu giá trị nguyên âm của tham số \(m\) để bất phương trình \({{3}^{x}}\ge \left( f\left( x \right)-m \right)\ln 3\) nghiệm đúng với mọi \(x\in \left( \frac{1}{2};+\infty  \right)\)?

• Cho số phức \(z=\frac{5}{2}-\frac{1}{2}i\). Tọa độ điểm \(M\) biểu diễn số phức \(z\) là