Cho hàm số \(y = \frac{{x - 1}}{{x + 1}}\) có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của (C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng

A. 3

B. 2

C. \(2\sqrt 2 .\)

D. \(2\sqrt 3 .\).

Suy nghĩ trả lời câu hỏi trước khi xem đáp án

Chủ đề: Đề thi THPT QG

Môn: Toán

Lời giải:

Báo sai

Ta có \(I\left( -1;1 \right)\)

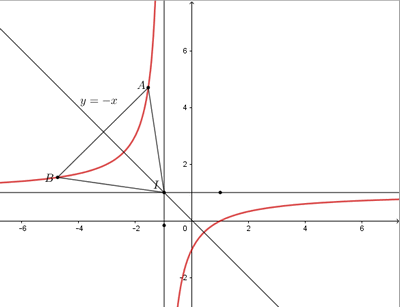
Tam giác \(IAB\) đều thì \(AB\) vuông góc với tia phân giác góc phần tư thứ \(II,IV\) : \(y = - x\)

Khi đó phương trình đường thẳng \(AB:y = x + m\), phương trình hoành độ giao điểm của \(\left( C \right)\) và \(AB\) là :

\(\frac{{x - 1}}{{x + 1}} = x + m \Leftrightarrow {x^2} + mx + m + 1 = 0\left( {x \ne - 1} \right)\,\,\left( 2 \right)\)

AB cắt (C) tại 2 điểm phân biệt khác – 1 khi và chỉ khi \(\left\{ \begin{array}{l}\Delta ' > 0\\{\left( { - 1} \right)^2} - m + m + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4m - 4 > 0\\2 \ne 0\left( {tm} \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 2 - 2\sqrt 2 \\m > 2 + 2\sqrt 2 \end{array} \right.\)

Gọi H là trung điểm của AB. Khi đó ta có IH cũng là trung tuyến của tam giác đều ABC

hay \(IH = \frac{{AB\sqrt 3 }}{2} = d\left( {I;AB} \right) \Leftrightarrow \frac{{AB\sqrt 3 }}{2} = \frac{{\left| { - 1 - 1 + m} \right|}}{{\sqrt 2 }} \Leftrightarrow \frac{{AB\sqrt 3 }}{2} = \frac{{\left| {m - 2} \right|}}{{\sqrt 2 }}\,\,\left( 3 \right)\)

Giả sử A, B lần lượt có tọa độ là : \(A\left( {{x_1};{x_1} + m} \right);B\left( {{x_2};{x_2} + m} \right) \Rightarrow AB = \sqrt {2{{\left( {{x_1} - {x_2}} \right)}^2}} = \sqrt {2\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \right]} \)

Áp dụng Viet cho phương trình (2) ta có : \(\left\{ \begin{array}{l}{x_1} + {x_2} = - m\\{x_1}{x_2} = m + 1\end{array} \right.\) .

Nên \(AB = \sqrt {2.\left( {{m^2} - 4m - 4} \right)} \)

Khi đó thay vào (3) ta có : \(\frac{{\sqrt {2.\left( {{m^2} - 4m - 4} \right).3} }}{2} = \frac{{\left| {m - 2} \right|}}{{\sqrt 2 }} \Leftrightarrow 3{m^2} - 12m - 12 = {m^2} - 4m + 4 \Leftrightarrow {m^2} - 4m - 8 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 2 - 2\sqrt 3 \\m = 2 + 2\sqrt 3 \end{array} \right.\)

Khi đó thay vào AB ta được \(AB = \sqrt 8 = 2\sqrt 2 .\)

Chọn C.

Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài