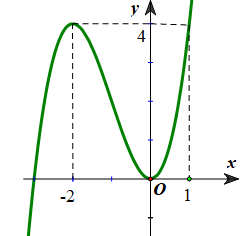
Cho hàm số \(y={{x}^{3}}-3x+2\) có đồ thị như hình dưới. Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \({{x}^{3}}-3x+2-2m=0\) có 3 nghiệm thực phân biệt?

Câu hỏi liên quan

• Cho biết \(\int\limits_{-1}^{2}{f\left( x \right)}\text{d}x=2\) và \(\int\limits_{1}^{2}{f\left( x \right)}\text{d}x=5\), tích phân \(\int\limits_{1}^{2}{f\left( 3-2x \right)}\text{d}x\) bằng?

• Trong không gian \(Oxyz\), tam giác \(ABC\) với \(A\left( 3;-1;2 \right)\), \(B\left( -1;3;5 \right)\) và \(C\left( 3;1;-3 \right)\). Đường trung tuyến \(AM\) của \(\Delta ABC\) có phương trình là?

• Đường cong trong hình bên là đồ thị của hàm số nào?

  

ZUNIA12

• Cho số phức \(z\) thỏa mãn \(\left( 1-i \right)\overline{z}=5+i\). Cho biết số phức \(\text{w}=2z+i\) là?

• Có tất cả bao nhiêu số phức \(z\) thỏa mãn \(3\left| z+\overline{z} \right|+2\left| z-\overline{z} \right|=12\) và \(\left| z+2-3i \right|=\left| \overline{z}-4+i \right|\)?

• Cho 1 chiếc cổng có dạng là một parabol \(\left( P \right)\) có kích thước như hình vẽ, biết chiều cao cổng bằng \(4\,m\,,\,AB\,=\,4\,m\). Người ta thiết kế cửa đi là một hình chữ nhật \(CDEF\,\), phần còn lại dùng để trang trí. Biết chi phí phần tô đậm là 1.000.000 đồng/\({{m}^{2}}\). Hỏi số tiền ít nhất dùng để trang trí phần tô đậm gần với số tiền nào dưới đây?

  

• Cho một vật chuyển động chậm dần đều với vận tốc \(v(t)=180-20t\,\left( m/s \right)\). Tính quãng đường mà vật di chuyển được từ thời điểm \(t=0\,(~s\,)\) đến thời điểm mà vật dừng lại?

• Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), cạnh \(SA\) vuông góc với mp đáy và \(SA=2a\), gọi \(M\) là trung điểm của \(SC\). Tính côsin của góc \(\alpha \) là góc giữa đường thẳng \(BM\) và \(\left( ABC \right)\)?

• Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng 1. Biết k/c từ \(A\) đến mp \(\left( SBC \right)\) là \(\frac{\sqrt{6}}{4}\), từ \(B\) đến mặt phẳng \(\left( SAC \right)\) là \(\frac{\sqrt{15}}{10}\), từ \(C\) đến mặt phẳng \(\left( SAB \right)\) là \(\frac{\sqrt{30}}{20}\).và hình chiếu vuông góc của \(S\) xuống đáy nằm trong tam giác \(ABC\). Thể tích khối chóp \(S.ABC\) bằng?

• Cho hàm số \(f\left( x \right)\) có bảng xét dấu đạo hàm như hình dưới. Hàm số \(y={{e}^{3f\left( 2-x \right)+1}}+{{3}^{f\left( 2-x \right)}}\) đồng biến trên khoảng nào?

  

• Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ 1\,;2 \right]\) thỏa mãn \(\int\limits_{1}^{2}{{{\left( x-1 \right)}^{2}}f\left( x \right)\text{d}x}=-\frac{1}{3}\), \(f\left( 2 \right)=0\) và \(\int\limits_{1}^{2}{{{\left[ {f}'\left( x \right) \right]}^{2}}\text{d}x}=7\). Tính tích phân của \(I=\int\limits_{1}^{2}{f\left( x \right)\text{d}x}\)?

• Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), \(\left( SAC \right)\bot \left( ABC \right)\) và \(AB=3a,\text{ }BC=5a\). Biết rằng \(SA=2a\sqrt{3}\) và \(\widehat{SAC}=30{}^\circ \). Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( SBC \right)\) bằng?

• Diện tích hình phẳng giới hạn bởi đồ thị của các HS \(y=2{{x}^{2}}+x+1\) và \(y={{x}^{2}}+3\) bằng?

• Trong không gian \(Oxyz\), mặt cầu có tâm \(I\left( -1;2;-3 \right)\) và đi qua điểm \(A\left( 2;0;0 \right)\) có phương trình là?

• Cho biết \(\int\limits_{0}^{1}{f(x)\text{d}x}=-3\) và \(\int\limits_{0}^{1}{g(x)\text{d}x}=2\), khi đó \(\int\limits_{0}^{1}{\left[ f\left( x \right)+2g\left( x \right) \right]\text{d}x}\) bằng?

• Cho phương trình \({{3}^{x}}\left( {{3}^{2x}}+1 \right)-\left( {{3}^{x}}+m+2 \right)\sqrt{{{3}^{x}}+m+3}=2\sqrt{{{3}^{x}}+m+3}\), với \(m\) là tham số. Có tất cả bao nhiêu giá trị nguyên âm của \(m\) để phương trình có nghiệm thực?

• Tính tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó bằng?

• Cho mặt cầu \(\left( S \right)\) có diện tích bằng \(4\pi \). Tính thể tích khối cầu \(\left( S \right)\)?

• Trong không gian \(Oxyz\), cho \(A\left( 0\,;\,1\,;\,1 \right)\), \(B\left( 2\,;\,-1\,;\,1 \right)\), \(C\left( 4\,;\,1\,;\,1 \right)\) và \(\left( P \right)\,:\,x+\,y+z-6\,=\,0\). Xét điểm \(M\left( a\,;\,b\,;\,c \right)\) thuộc \(\left( P \right)\) sao cho \(\left| \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC} \right|\) đạt GTNN. Giá trị của \(\,2a+4b+c\) bằng?

• Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) cạnh bằng 1. Gọi \(M\) là trung điểm cạnh \(B{B}'\). Mặt phẳng \(\left( M{A}'D \right)\) cắt cạnh \(BC\) tại \(K\). Tính thể tích của khối đa điện \({A}'{B}'{C}'{D}'MKCD\)?