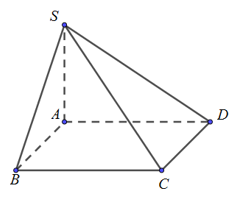
Cho hình chóp S.ABCD, có đáy là hình chữ nhật, \(AB=a,\,\,AD=2a\), cạnh bên \(SA=a\) và \(SA\) vuông góc với đáy. Khoảng cách từ A đến mặt phẳng (SBD) bằng
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Kẻ \(AH\bot BD\,\,(H\in BD),\,\,AK\bot SH\,\,(K\in SH)\)
Ta có: \(\left\{ \begin{align} & BD\bot AH \\ & BD\bot AS \\\end{align} \right.\Rightarrow BD\bot (SAH)\Rightarrow BD\bot AK\)
Mặt khác : \(\left\{ \begin{align} & AK\bot SH \\ & AK\bot BD \\\end{align} \right.\Rightarrow AK\bot (SBD)\Rightarrow d(A;(SBD))=AK\)
\(\Delta ABD\) vuông tại A, \(AH\bot BD\Rightarrow \frac{1}{A{{H}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{A{{D}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{4{{a}^{2}}}=\frac{5}{4{{a}^{2}}}\)
\(\Delta SAH\) vuông tại A, \(AK\bot SH\Rightarrow \frac{1}{A{{K}^{2}}}=\frac{1}{A{{H}^{2}}}+\frac{1}{S{{A}^{2}}}=\frac{5}{4{{a}^{2}}}+\frac{1}{{{a}^{2}}}=\frac{9}{4{{a}^{2}}}\Rightarrow AK=\frac{2a}{3}\)
\(\Rightarrow d(A;(SBD))=AK=\frac{2a}{3}\).
Chọn: C
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Nguyễn Hữu Thọ











