Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D ,\(S A \perp(A B C D)\) . Góc giữa SB và mặt phẳng đáy bằng 45°, E là trung điểm của SD , \(A B=2 a, A D=D C=a\) . Tính khoảng cách từ B đến ( ACE) .
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai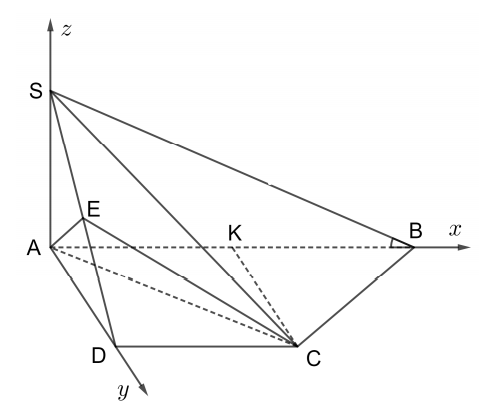
\((\widehat{S B,(A B C D)})=45^{0} \Rightarrow \widehat{S B A}=45^{0} \Rightarrow\) Tam giác SAB vuông cân tại A \(\Rightarrow S A=A B=2 a\)
Chọn hệ trục Axyz như hình vẽ. Ta được \(A(0 ; 0 ; 0), \) \(S(0 ; 0 ; 2 a), B(2 a ; 0 ; 0), D(0 ; a ; 0)\)
Gọi K là trung điểm của AB . Nhận xét rằng tứ giác ADCK là hình chữ nhật \(\Rightarrow C(a ; a ; 0)\).
E là trung điểm của SD \(\Rightarrow E\left(0 ; \frac{a}{2} ; a\right)\)
\([\overrightarrow{A E}, \overrightarrow{A C}]=\left(-a^{2} ; a^{2} ;-\frac{a^{2}}{2}\right)=-\frac{a^{2}}{2}(2 ;-2 ; 1)\)
Mặt phẳng ( ACE) đi qua A(0;0;0) và nhận vectơ \((2 ;-2 ; 1)\) là một vectơ pháp tuyến nên có phương trình \(2 x-2 y+z=0\)
Vậy khoảng cách từ B đến (ACE)
\(\mathrm{d}(B,(A C E))=\frac{|2.2 a|}{\sqrt{2^{2}+(-2)^{2}+1^{2}}}=\frac{4 a}{3}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Trần Phú lần 2