Cho hình hộp chữ nhật \(ABCD.{A}'{B}'{C}'{D}'\) có \(A{A}'=AD=a\), \(AB=a\sqrt{2}\) (tham khảo hình). Góc giữa đường thẳng \({A}'C\) và mặt phẳng \(\left( ABB'A' \right)\) bằng?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
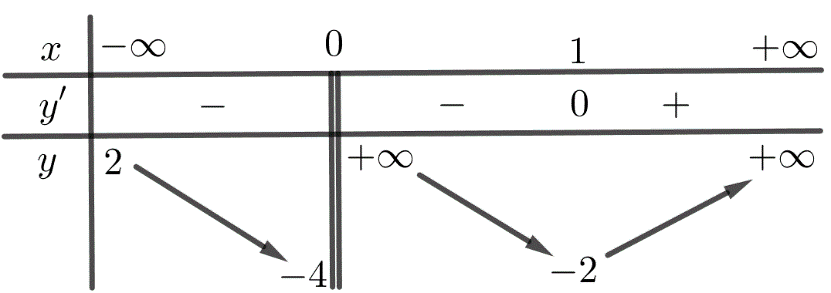
Báo saiVì \(ABB'A'\) là hình chữ nhật, có \(AA'=a\), \(AB=a\sqrt{2}\) nên
\(A'B=\sqrt{AA{{'}^{2}}+A{{B}^{2}}}\)\( =\sqrt{{{a}^{2}}+{{\left( a\sqrt{2} \right)}^{2}}}\)\( =a\sqrt{3}\)
Ta có \(BC\bot \left( ABB'A' \right)\widehat{\Rightarrow \left( {A}'C;\left( ABB'A' \right) \right)}\)\( =\widehat{\left( {A}'C;A'B \right)}\)\( =\widehat{B{A}'C}\)
Do tam giác \(B{A}'C\) vuông tại \(B\) nên \(\tan \widehat{B{A}'C}\)\( =\frac{BC}{A'B}\)\( =\frac{a}{a\sqrt{3}}\)\( =\frac{1}{\sqrt{3}}\) \(\Rightarrow \) \(\widehat{B{A}'C}={{30}^{\circ }}\).
Chọn A
Đề thi thử tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Lương Văn Can
.PNG)
.PNG)