Cho lăng trụ tam giác \(A B C \cdot A^{\prime} B^{\prime} C^{\prime} \operatorname{có} B B^{\prime}=a\), góc giữa BB' và mặt phẳng (ABC) bằng \(30^o\). Hình chiếu vuông góc của B' lên mp (ABC) trùng với trọng tâm tam giác ABC. Tính khoảng cách từ A đến mặt phẳng (A'B'C').
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai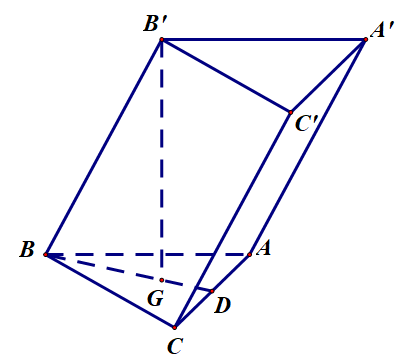
Gọi G là trọng tâm tam giác ABC và D là trung điểm AC thì \(\mathrm{B}^{\prime} \mathrm{G} \perp(\mathrm{ABC})\)
Khi đó góc giữa BB' và (ABC) là \(\widehat{B'BG}\)
Khoảng cách từ A đến mặt phẳng (A’B’C’) bằng khoảng cách từ B’ đến mặt phẳng (ABC) .
\(d_{(B ;(A B C))}=B^{\prime} G ; \widehat{B^{\prime} B G}=30^{0} \)
\(\text { nên } B^{\prime} G=BB'.sin30^o=\frac{a}{2} \Rightarrow d{\left(A ;\left(a^{\prime} B^{\prime} C\right)\right)}=\frac{a}{2}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Nho Quan B