Cho \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y={{x}^{2}}-4x+4\), trục hoành và trục tung. Đường thẳng \(d\) qua \(A\left( 0\,;\,4 \right)\) và có hệ số góc \(k\,\,\left( k\in \mathbb{R} \right)\) chia hình \(\left( H \right)\) thành hai phần có diện tích bằng nhau. Giá trị của \(k\) bằng

Câu hỏi liên quan

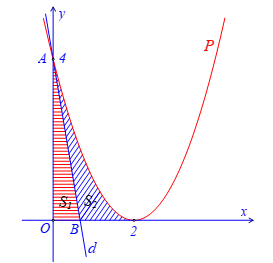
• Số nghiệm nguyên của bất phương trình \({{\log }_{\frac{1}{4}}}\left( x-1 \right)+{{\log }_{4}}\left( 14-2x \right)\ge 0\) là

• Môđun của số phức \(z=4-3i\) bằng

• Có bao nhiêu cặp số nguyên \(\left( x\,;\,y \right)\) thỏa mãn \({{2.3}^{x-1}}-{{\log }_{3}}\left( {{3}^{x-2}}+2y \right)=6y-x\,+1\) và \({{2022}^{-1}}\le y\le 2022\)?

ZUNIA12

• Cho hai số phức  \({{z}_{1}}=2+3i\) và \({{z}_{2}}=3-2i\). Số phức \({{z}_{1}}.{{z}_{2}}\) bằng

• Cho hàm số \(y=f(x)\) có đồ thị là đường cong như hình bên dưới.

  

  Đồ thị hàm số đã cho cắt trục hoành tại điểm nào sau đây?

• Cho cấp số cộng \(\left( {{u}_{n}} \right)\)biết \({{u}_{1}}=5,\,{{u}_{2}}=8\). Giá trị của \({{u}_{4}}\) bằng 

• Một hộp chứa 9 quả cầu gồm 4 quả màu xanh, 3 quả màu đỏ và 2 quả màu vàng. Lấy ngẫu nhiên 3 quả cầu từ hộp đó. Xác suất để trong 3 quả cầu lấy được có ít nhất một quả màu đỏ bằng

• Cho \({{\log }_{a}}5=3\), khi đó giá trị của \({{\log }_{{{a}^{2}}}}\left( 5{{a}^{3}} \right)\) bằng

• Với \(a\) là số thực dương, \(\log {{a}^{10}}\) bằng

• Cho các số phức \(w,\,z\) thỏa mãn \(\left| w+i \right|=\frac{3\sqrt{5}}{5}\) và \(5w=\left( 2+i \right)\left( z-4 \right)\). Giá trị lớn nhất của biểu thức \(P=\left| z-1-2i \right|+\left| z-5-2i \right|\) bằng

• Hàm số \(y=\frac{{{x}^{3}}}{3}-2{{x}^{2}}+3x+1\) nghịch biến trên khoảng nào dưới đây?

• Giá trị lớn nhất của hàm số \(f\left( x \right)=2{{x}^{3}}-6x\) trên đoạn \(\left[ 0;2 \right]\) bằng

• Trong không gian \(Oxyz,\)gọi \(\left( P \right)\) là mặt phẳng chứa đường thẳng \(d:\frac{x-2}{1}=\frac{y-1}{2}=\frac{z}{-1}\) và cắt trục \(Ox\,,\,Oy\) lần lượt tại \(A\) và \(B\) sao cho đường thẳng \(AB\) vuông góc với \(d\). Phương trình của mặt phẳng \(\left( P \right)\) là

• Tập xác định của hàm số \(y={{\log }_{3}}\left( {{x}^{2}}-1 \right)\) là

• Cho khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=4\). Thể tích của khối chóp đã cho bằng

• Thể tích của khối cầu có bán kính \(R\) là 

• Số cách xếp 4 người thành một hàng ngang là

• Cho khối nón đỉnh \(S\) có đáy là đường tròn tâm \(O\), bán kính \(R\). Trên đường tròn \(\left( O \right)\) lấy hai điểm \(A,B\) sao cho tam giác \(OAB\) vuông. Biết diện tích tam giác \(SAB\) bằng \(\sqrt{2}{{R}^{2}}\). Thể tích khối nón đã cho bằng

• Trên tập hợp số phức, biết \({{z}_{0}}=3-2i\) là một nghiệm của phương trình \({{z}^{2}}+az+b=0\)(với \(a,\,\,b\in \mathbb{R}\)). Giá trị của \(a+b\) bằng

• Trong không gian \(Oxyz\), điểm nào dưới đây thuộc đường thẳng \(d:\frac{x-1}{2}=\frac{y}{1}=\frac{z+1}{2}?\)