Cho mạch điện như hình vẽ. Đặt vào hai đầu A, B một điện áp xoay chiều có giá trị hiệu dụng U và tần số f không đổi. Điều chỉnh C để tổng điện áp hiệu dụng UAM + UMB lớn nhất thì tổng đó bằng 2U và khi đó công suất tiêu thụ của đoạn mạch AM là 36 W. Tiếp tục điều chỉnh C để công suất tiêu thụ của đoạn mạch lớn nhất thì công suất lớn nhất đó bằng
.png)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai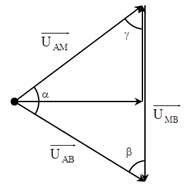
+ Biểu diễn vecto các điện áp.
+ Áp dụng định lý sin trong tam giác, ta có:
\(\frac{{{U}_{AM}}}{\sin \beta }=\frac{{{U}_{MB}}}{\sin \alpha }=\frac{{{U}_{AB}}}{\sin \gamma }=\frac{{{U}_{AM}}+{{U}_{MB}}}{\sin \alpha +\sin \beta }\to {{U}_{AM}}+{{U}_{MB}}=\frac{{{U}_{AB}}}{\sin \gamma }\left( \sin \alpha +\sin \beta \right)\)
với \(\gamma \) luôn không đổi.
\({{U}_{AM}}+{{U}_{MB}}=\frac{2{{U}_{AB}}}{\sin \gamma }\sin \left( \frac{\alpha +\beta }{2} \right)\cos \left( \frac{\alpha -\beta }{2} \right)=\frac{2{{U}_{AB}}}{\sin \gamma }\sin \left( \frac{180-\gamma }{2} \right)c\text{os}\left( \frac{\alpha \text{-}\beta }{\text{2}} \right)\)
\(\to {{\left( {{U}_{AM}}+{{U}_{MB}} \right)}_{\max }}\) khi \(\alpha =\beta .\)
=> \({{\left( {{U}_{AM}}+{{U}_{MB}} \right)}_{\max }}=\frac{2U}{\sin \gamma }\sin \left( \frac{180-\gamma }{2} \right)=2U\to \gamma =60{}^\circ .\)
\(\to \) Các vecto hợp với nhau thành tam giác đều \(\to \) khi xảy ra cực đại u chậm pha hơn i một góc \(30{}^\circ \).
\(P={{P}_{\max }}{{\cos }^{2}}\varphi \to {{P}_{\max }}=\frac{P}{{{\cos }^{2}}\varphi }=\frac{36}{{{\cos }^{2}}30{}^\circ }=48\,\,W.\)
Câu hỏi liên quan
-
Trong quá trình truyền tải điện năng biện pháp giảm hao phí trên đường dây tải điện được sử dụng chủ yếu hiện nay là
-
Sóng (cơ học) ngang:
-
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn S phát ra ba ánh sáng đơn sắc: 0,42μm(màu tím); 0,56μm (màu lục); 0,70μm (màu đỏ). Số vân tím, vân lục và vân đỏ nằm giữa hai vân sáng liên tiếp có màu giống như màu của vân trung tâm là:
-
Tại hai điểm A và B trên mặt nước cách nhau 16 cm có hai nguồn giống nhau. Điểm M nằm trên mặt nước và nằm trên đường trung trực của AB, cách trung điểm I của AB một khoảng nhỏ nhất bằng 4\(\sqrt{5}\)cm luôn dao động cùng pha với I. Điểm N nằm trên mặt nước và nằm trên đường thẳng vuông góc với AB tại A, cách A một khoảng nhỏ nhất bằng bao nhiêu để N dao động với biên độ cực tiểu?
-
Lần lượt chiếu hai bức xạ có bước sóng λ1 = 0,75 μm và λ2 = 0,25 μm vào một tấm kẽm có giới hạn quang điện λo = 0,35 μm. Bức xạ nào gây ra hiện tượng quang điện ?
-
Trong các ánh sáng đơn sắc sau đây. Ánh sáng nào có khả năng gây ra hiện tượng quang điện mạnh nhất?
-
Đặt điện áp u = U0cos100πtV vào hai đầu đoạn mạch A, B gồm cuộn dây thuần cảm, có độ tự cảm \(L=\frac{1}{4\pi }H\) và tụ có điện dung \(C=\frac{400}{3\pi }\mu F\) mắc nối tiếp. Tại thời điểm điện áp tức thời giữa hai đầu tụ điện bằng 120 V thì điện áp tức thời giữa hai đầu A, B có giá trị bằng
-
Kim loại làm catốt của một tế bào quang điện có giới hạn quang điện là λo. Chiếu lần lượt tới bề mặt catốt hai bức xạ có bước sóng λ1 = 0,4 μm và λ2 = 0,5 μm thì vận tốc ban đầu cực đại của các electron bắn ra khác nhau 1,5 lần. Bước sóng λo là
-
Nếu chiếu một chùm tia hồng ngoại vào tấm kẽm tích điện âm, thì
-
Trong thí nghiệm giao thoa ánh sáng với khe Y âng, khoảng cách giữa hai khe là 2mm, khoảng cách từ hai khe đến màn là 3m. Nguồn phát ra ánh sáng đơn sắc có bước sóng \(\lambda \). Ban đầu thí nghiệm được thực hiện trong không khí. Sau đó nhúng toàn bộ thí nghiệm trong nước thì khoảng vân giảm đi 0,25mm so với ban đầu. Chiết suất của nước đối với ánh sáng đơn sắc bằng 1,5. Bước sóng ánh sáng bằng bao nhiêu?
-
Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là
-
Trong thí nghiệm Y-âng, hai khe được chiếu bằng ánh sáng trắng ( có bước sóng từ 0,4μm đến 0,6 μm ). Khi đó tại vị trí của vân sáng bậc 4 của ánh sáng đỏ ( λ = 0,76 μm ) còn có bao nhiêu bức xạ đơn sắc cho vân sáng tại đó ?
-
Hai dao động điều hòa có đồ thị li độ - thời gian như hình vẽ. Tổng vận tốc tức thời của hai dao động có giá trị lớn nhất là
.png)
-
Điện năng từ nhà máy được đưa tới nơi tiêu thụ nhờ các dây dẫn. Biết công suất truyền đi là không đổi. Ban đầu hiệu suất truyền tải điện là 80%. Muốn hiệu suất truyền tải điện là 85% thì cần giảm cường độ dòng điện trên dây tải đi
-
Một con lắc lò xo nằm ngang gồm vật nặng M = 200 g và độ cứng lò xo k = 40 N/m có thể trượt không ma sát trên mặt phẳng nằm ngang. Khi hệ đang ở trạng thái cân bằng thì có một vật khối lượng m = 200 g chuyển động đến va chạm mềm vào M theo phương ngang với tốc độ 3 m/s. Sau va chạm hệ dao động điều hòa với biên độ là
-
Trong trường hợp nào sau đây ta có thể coi các vật nhiễm điện là các điện tích?
-
Dòng điện trong cuộn tự cảm giảm từ 16A đến 0A trong thời gian 0,01s. Suất điện động tự cảm trong cuộn đó có giá trị trung bình là 64V. Khi đó độ tự cảm có giá trị là :
-
Một sóng ngang có chu kì T = 0,2 s truyền trong một môi trường đàn hồi có tốc độ 1 m/s. Xét trên phương truyền sóng Ox, vào một thời điểm nào đó một điểm M nằm tại đỉnh sóng thì ở sau M theo chiều truyền sóng, cách M một khoảng từ 42 cm đến 60 cm có điểm N đang từ vị tri cân bằng đi lên đỉnh sóng. Khoảng cách MN là:
-
Đặt vào hai đầu đoạn mạch RLC nối tiếp một hiệu điện thế xoay chiều u = Uo sinωt thì độ lệch pha của hiệu điện thế u với cường độ dòng điện i trong mạch được tính theo công thức
-
Trong thí nghiệm về sóng dừng, trên một sợi dây đàn hồi dài 1,2m với hai đầu cố định, người ta quan sát thấy ngoài hai đầu dây cố định còn có hai điểm khác trên dây không dao động. Biết khoảng thời gian giữa hai lần liên tiếp với sợi dây duỗi thẳng là 0,05s. Tốc độ truyền sóng trên dây là
