Có bao nhiêu giá trị \(m\) nguyên trong \(\left[ -2022;2022 \right]\)để phương trình \(\log \left( mx \right)=2\log \left( x+1 \right)\)có nghiệm duy nhất?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn A
Điều kiện: \(\left\{ \begin{align} & mx>0 \\ & x>-1 \\ \end{align} \right.\)
Phương trình suy ra: \(mx={{\left( x+1 \right)}^{2}}\)\(\Leftrightarrow m=\frac{{{\left( x+1 \right)}^{2}}}{x},\,\,\left( x\ne 0 \right)\)
Xét hàm số \(f\left( x \right)=\frac{{{\left( x+1 \right)}^{2}}}{x}\) trên khoảng \(\left( -1;\,+\infty \right)\backslash \left\{ 0 \right\}\)
Ta có: \({f}'\left( x \right)=1-\frac{1}{{{x}^{2}}}\), \({f}'\left( x \right)=0\Rightarrow x=\pm 1\)
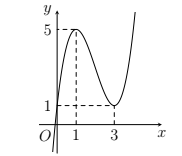
BBT của hàm số \(f\left( x \right)\) trên khoảng \(\left( -1;\,+\infty \right)\backslash \left\{ 0 \right\}\)
Từ bảng biến thiên, để phương trình có nghiệm duy nhất khi
\(\left[ \begin{align} & m=4 \\ & m<0 \\ \end{align} \right.\)
Kết hợp với điều kiện \(m\in \mathbb{Z}\) và \(m\in \left[ -2022;\,2022 \right]\) ta có:
\(m=\left\{ -2022;\,-2021;.....;\,-1;\,4 \right\}\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Chuyên Trần Phú
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)











