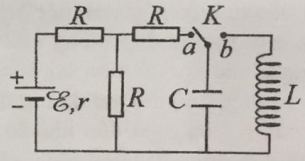
Dùng mạch điện như hình bên để tạo ra dao động điện từ. Ban đầu khóa K vào chốt a, khi dòng điện qua nguồn điện ổn định thì chuyển khóa K đóng sang chốt b. Biết x = 5 V; r = 1 W; R = 2 W; \(L=\frac{1}{\pi }\,mH\) và \(C=\frac{9}{10\pi }\,\mu F\). Lấy 1 e = 1,6.10-19 C. Trong khoảng thời gian 10 ms kể từ thời điểm đóng K vào chốt b, có bao nhiêu electron đã chuyển đến bản tụ điện nối với khóa K?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai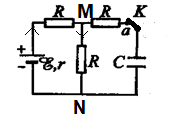
Khi khóa K ở chốt a, ta có hiệu điện thế ở hai đầu tụ điện là :
U0 = UMN = I.R
\(I=\frac{\xi }{2R+r}\to {{U}_{0}}=\frac{\xi }{2R+r}.R=\frac{5}{2.2+1}.2=2\,V\)
Khi khóa K ở chốt b, ta có mạch dao động LC với chu kì:
\(T=2\pi \sqrt{LC}=2\pi \sqrt{\frac{{{10}^{-3}}}{\pi }.\frac{{{9.10}^{-6}}}{10\pi }}={{6.10}^{-5}}s=60\,\mu s\)
Phương trình điện tích khi đóng K vào chốt b là:
q = q0.coswt (C) (j = 0 do ban đầu điện tích cực đại)
Sau thời gian 10 ms :
\(t=10\,\mu s=\frac{T}{6}\) thì \(q=\frac{{{q}_{0}}}{2}\)
Lượng điện tích chuyển đến tụ là: \(\Delta q={{q}_{0}}-\frac{{{q}_{0}}}{2}=\frac{{{q}_{0}}}{2}=\frac{C{{U}_{0}}}{2}\)
Số electron chuyển đến bản tụ là: \(\Delta n=\frac{\Delta q}{e}=\frac{C{{U}_{0}}}{2e}=\frac{\frac{{{9.10}^{-6}}}{10\pi }.2}{2.1,{{6.10}^{-19}}}\approx 1,{{79.10}^{12}}\)