Một con lắc lò xo nằm ngang gồm vật m = 0,1 kg, k = 100N/m. Từ vị trí lò xo không biến dạng đẩy vật sao cho lò xo nén 2 √ 3 cm rồi buông nhẹ, khi vật đi qua vị trí lò xo không biến dạng lần đầu tiên tác dụng lực F = 2N không đổi cùng chiều vận tốc của vật, khi đó vật dao động điều hòa với biên độ A1, sau 1/30 s kể từ khi tác dụng lực F, ngừng tác dụng lực F, khi đó vật dao động với A2, tính A2/A1. Lấy π2 = 10.
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChu kì dao động của con lắc lò xo:
\(T = 2\pi \sqrt {\frac{m}{k}} = \frac{1}{5}\)(s)
+ Khi chưa có lực vật dao động với biên độ A = 2 √3 xung quanh vị trí cân bằng O. Khi vật đến O có lực tác dụng F, lúc này vị trí cân bằng dịch đi đoạn
\({x_0} = \frac{F}{k} = 0,02\left( m \right) = 2\left( {cm} \right)\) đến vị trí O1 theo chiều hướng tác dụng.
+ Vậy, tại thời điểm tác dụng lực vật có li độ và vận tốc là:
\(\left\{ \begin{array}{l}
{x_0} = - 2\left( {cm} \right)\\
{v_0} = \omega A
\end{array} \right.\)
+ Do đó biên độ dao dộng của vật lúc này là:
\({A_1} = \sqrt {x_0^2 + \frac{{v_0^2}}{{{\omega ^2}}}} = \sqrt {x_0^2 + {{\left( {\frac{{\omega A}}{\omega }} \right)}^2}} = \sqrt {x_0^2 + {A^2}} = 4\left( {cm} \right)\)
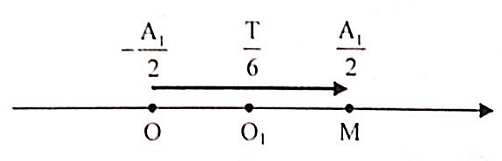
+ Vậy sau khi tác dụng lực F vật dao động với biên độ A1 = 4 cm xung quanh VTCB O1. Khi tác dụng lực F vật đang ở O có li độ
\({x_1} = - \frac{{{A_1}}}{2} = - 2\left( {cm} \right);\Delta t = \frac{1}{{30}}\left( s \right) = \frac{T}{6}\)
vật sẽ đến M có li độ \({x_2} = \frac{{{A_1}}}{2} = 2\left( {cm} \right)\).
Khi đến M thì mất lực tác dụng nên VTCB lại về O, lúc đó vật có li độ và vận tốc là:
\(\left\{ \begin{array}{l}
x = 4\left( {cm} \right)\\
v = \frac{{\omega {A_1}\sqrt 3 }}{2}
\end{array} \right.\)
+ Vậy biên độ dao động sau khi bỏ lực là:
\({A_2} = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{4^2} + \frac{3}{4}{4^2}} = 2\sqrt 7 \Rightarrow \frac{{{A_2}}}{{{A_1}}} = \frac{{\sqrt 7 }}{2}\)
Đề thi thử THPT QG năm 2021 môn Vật Lý
Trường THPT Trần Hữu Trang











