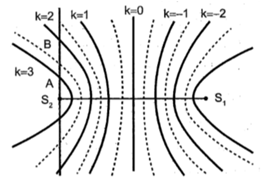
Trên mặt chất lỏng, có hai nguồn kết hợp \({{S}_{1}}\)  và \({{S}_{2}}\) cách nhau 16 cm, dao động theo phương thẳng đứng với phương trình \({{u}_{1}}={{u}_{2}}=2.\cos \left( 10\pi t \right)\left( mm \right)\). Tốc độ truyền sóng trên mặt chất lỏng là 20 cm/s. Coi biên độ sóng không đổi khi truyền đi. Trên đường thẳng vuông góc với \({{S}_{1}}{{S}_{2}}\) tại điểm \({{S}_{2}}\) lấy điểm M sao cho \(M{{S}_{1}}=34cm\)  và \(M{{S}_{2}}=30cm.\) Điểm A và B lần lượt nằm trong khoảng \({{S}_{2}}M\)  với A gần \({{S}_{2}}\)  nhất, B xa \({{S}_{2}}\) nhất, đều có tốc độ dao động cực đại bằng 12,57cm/s. Khoảng cách AB là

Câu hỏi liên quan

• Đại lương nào không thay đổi khi sóng cơ truyền từ môi trường đàn hồi này sang môi tường đàn hồi khác?

• Máy biến áp là một thiết bị:

• Cho ba con lắc lò xo dao động điều hòa theo phương nằm ngang. Biết ba lò xo giống hệt nhau và vật nặng có khối lượng tương ứng là \({{m}_{1}},{{m}_{2}}\) và \({{m}_{3}}\) . Lần lượt kéo ba vật sao cho ba lò xo giãn cùng một đoạn A như nhau rồi thả nhẹ cho ba vật dao động điều hòa. Khi đi qua vị trí cân bằng vận tốc của hai vật \({{m}_{1}},{{m}_{2}}\) có độ lớn lần lượt \({{v}_{1}}=20cm/s,\,\,{{v}_{2}}=10cm/s.\)  Biết \({{m}_{3}}=9{{m}_{1}}+4{{m}_{2}}\), độ lớn vận tốc cực đại của vật \({{m}_{3}}\)  là

ZUNIA12

• Đặt một điện áp xoay chiều \(u=150\sqrt{2}\cos \omega t\) vào hai đầu đoạn mạch R, L, C mắc nối tiếp có L biến thiên. Điều chỉnh L để điện áp hiệu dụng giữa hai đầu điện trở R, cuộn cảm L, tụ điện C lần lượt đạt cực đại thì các giá trị cực đại đó lần lượt là \({{U}_{1}},{{U}_{2}},{{U}_{3}}.\)  Biết \({{U}_{1}},{{U}_{2}}\) chênh nhau 3 lần. Giá trị \({{U}_{3}}\) là

• Theo thuyết lượng tử ánh sáng thì năng lượng của

• Kẻ trộm giấu viên kim cương ở dưới đáy bể bơi. Anh ta đặt chiếc bè mỏng đồng chất hình tròn bán kính R trên mặt nước, tâm của bè nằm trên đường thẳng đứng đi qua viên kim cương. Mặt nước yên lặng và mức nước là \(h=2,5m.\)  Cho chiết suất của nước là \(n=\frac{4}{3}\) . Giá trị nhỏ nhất của R để người ở ngoài bể bơi không nhìn thấy viên kim cương gần đúng bằng

  

• Một sóng cơ học truyền dọc theo một sợi dây đàn hồi với tốc độ 25m/s và có tần số dao động là 5 Hz. Sóng truyền trên dây có bước sóng là

• Cho một mạch dao động LC lí tưởng gồm cuộn dây thuần cảm có L = 2mH và tụ điện có điện dung C= 2nF. Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì dòng điện trong mạch có độ lớn \(3\sqrt{2}A.\)  Lấy chiều dương của dòng điện sao cho dòng điện i sớm pha so với hiệu điện thế trên tụ điện, gốc thời gian là lúc dòng điện trong mạch có giá trị bằng 1 nửa giá trị cực đại và tụ điện đang được nạp điện. Biểu thức của cường độ dòng điện trong mạch là:

• Một con lắc lò xo gồm viên bi nhỏ có khối lượng m và lò xo có khối lượng không đáng kể, có độ cứng 50 N/m. Con lắc dao động cưỡng bức dưới tác dụng của ngoại lực tuần hoàn có tần số \({{\omega }_{F}}\). Biết biên độ dao động của ngoại lực tuần hoàn không thay đổi. Khi thay đổi \({{\omega }_{F}}\) thì biên độ dao động của viên bi thay đổi và khi \({{\omega }_{F}}=25rad/s\) thì biên độ dao động của viên bi đạt giá trị cực đại. Khối lượng m của viên bi bằng

• Tâm của vòng dây tròn có dòng điện cường độ 5A cảm ứng từ được đo là \(31,{{4.10}^{-6}}T.\) Đường kính của vòng dây điện đó là

• Cho mạch gồm R, L, C mắc nối tiếp. Đặt điện áp xoay chiều u vào đoạn mạch. Gọi \({{u}_{1}},{{u}_{2}},{{u}_{3}}\) lần lượt là điện áp tức thời giữa hai đầu điện trở thuần, cuộn dây, tụ điện. Kết luận nào sau đây là đúng?

• Người ta mắc hai cực của nguồn điện với một biến trở có thể thay đổi từ 0 đến vô cực. Khi giá trị của biến trở rất lớn thì hiệu điện thế giữa hai cực của nguồn điện là 4,5V. Giảm giá trị của biến trở đến khi cường độ dòng điện trong mạch là 2A thì hiệu điện thế giữa hai cực của nguồn điện là 4V. Suất điện động và điện trở trong của nguồn điện là

• Hạt proton có năng lượng toàn phần lớn gấp 3 lần năng lượng nghỉ của nó. Tốc độ của hạt proton này là:

• Một mạch dao động lí tưởng gồm cuộn dây thuần cảm có độ tự cảm L không đổi và tụ điện có điện dung C thay đổi được. Khi điện dung của tụ là \({{C}_{1}}\) thì tần số dao động riêng của mạch là 30 Hz. Từ giá trị \({{C}_{1}}\) nếu điều chỉnh tăng thêm điện dung của tụ một lượng \(\Delta C\) thì tần số dao động riêng của mạch là 2f.  Từ giá trị \({{C}_{1}}\) nếu điều chỉnh tăng thêm điện dung của tụ một lượng \(9\Delta C\) thì chu kì dao động riêng của mạch là

• Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây N là một điểm nút, B là một điểm bụng gần N nhất. NB = 25 cm, gọi C là một điểm trên NB có biên độ \({{A}_{C}}=\frac{{{A}_{B}}\sqrt{3}}{2}\). Khoảng cách NC là

• Khi nói về sự phóng xạ, phát biểu nào sau đây là đúng?

• Trong giờ thực hành khảo sát các định luật của con lắc đơn tại phòng thực hành của trường X. Học sinh sử dụng 1 con lắc đơn có độ dài l (cm) và quan sát thấy trong khoảng thời gian \(\Delta t\) con lắc thực hiện được 15 dao động. Học sinh giảm bớt chiều dài của nó đi 28cm thì cũng trong khoảng thời gian đó học sinh quan sát thấy con lắc thực hiện được 20 dao động. Chiều dài ban đầu của con lắc bằng bao nhiêu?

• Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, vuông pha nhau, có biên độ tương ứng là \({{A}_{1}}\) và \({{A}_{2}}\) . Biết dao động tổng hợp có phương trình \(x=16\cos \left( \omega t \right)\left( cm \right)\) và lệch pha so với dao động thứ nhất một góc \({{\alpha }_{1}}\) . Thay đổi biên độ của hai dao động, khi biên độ của dao động thứ hai tăng lên \(\sqrt{15}\) lần so với ban đầu (nhưng vẫn giữ nguyên pha của hai dao động thành phần) thì dao động tổng hợp có biên độ không đổi nhưng lệch pha so với dao động thứ nhất một góc là \({{\alpha }_{2}}\) với \({{\alpha }_{1}}+{{\alpha }_{2}}=\frac{\pi }{2}\) . Giá trị ban đầu của biên độ \({{A}_{2}}\) là

• Cho mạch điện xoay chiều gồm R, L, C mắc nối tiếp, cuộn dây thuần cảm. Các giá trị điện trở R, độ tự cảm L và điện dung C của tụ điện thỏa mãn điều kiện \(3L=C{{R}^{2}}.\) Đặt vào hai đầu đoạn mạch điện áp xoay chiều ổn định, tần số của dòng đện thay đổi được. Khi tần số của dòng điện là \({{f}_{1}}=50Hz\) thì hệ số công suất của mạch điện là \({{k}_{1}}\). Khi tần số \({{f}_{2}}=150Hz\) thì hệ số công suất của mạch điện là \({{k}_{2}}=\frac{5}{3}{{k}_{1}}\) . Khi tần số \({{f}_{3}}=200Hz\) thì hệ số công suất của mạch là \({{k}_{3}}\) . Giá trị của \({{k}_{3}}\) gần với giá trị nào nhất sau đây?

• Dùng hạt \(\alpha \) có động năng K bắn vào hạt nhân \(_{7}^{14}N\) đứng yên gây ra phản ứng: \(_{2}^{4}He+_{7}^{14}N\to X+_{1}^{1}H\) . Phản ứng này thu được năng lượng 1,21MeV và không kèm theo bức xạ gam-ma. Lấy  khối lượng các hạt nhân tính theo đơn vị u bằng số khối của chúng. Hạt nhân X và hạt nhân \(_{1}^{1}H\)  bay ra theo các hướng hợp với hướng chuyển động của hạt \(\alpha \) các góc lần lượt \({{20}^{o}}\)  và \({{70}^{o}}\) . Động năng của hạt nhân \(_{1}^{1}H\) là