Trong không gian \(\text{Ox}yz\), cho mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{\left( z+1 \right)}^{2}}=5\). Có tất cả bao nhiêu điểm \(A\left( a\,;\,b\,;\,c \right)\) ( \(a\,,\,b\,,\,c\) là các số nguyên) thuộc mặt phẳng \(\left( Oxy \right)\) sao cho có ít nhất hai tiếp tuyến của \(\left( S \right)\) đi qua A và hai tiếp tuyến đó vuông góc với nhau?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐáp án A
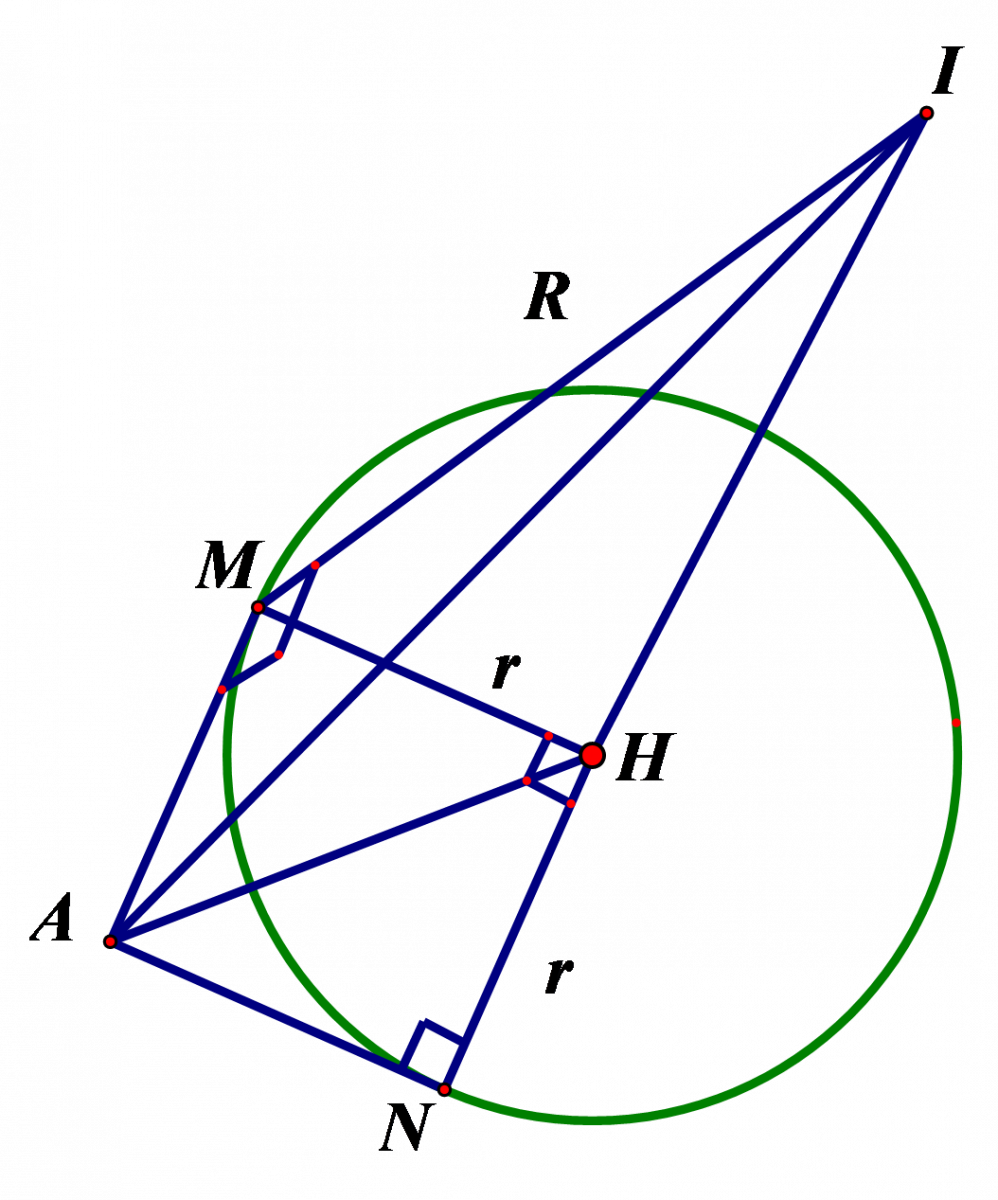
Gọi \(M\,,\,N\) là tiếp điểm, H là tâm của đường tròn giao tuyến giữa mặt phẳng \(\left( AMN \right)\) và mặt cầu \(\left( S \right)\), r là bán kính của đường tròn giao tuyến.
Ta có: \(AM=MH=r\,\).
Dễ thấy: \(I{{M}^{2}}+M{{A}^{2}}=A{{I}^{2}}\Rightarrow {{R}^{2}}+{{r}^{2}}=A{{I}^{2}}\).
Do \(0\le r\le R\Rightarrow {{R}^{2}}\le A{{I}^{2}}\le 2{{R}^{2}}\)
Với giả thiết bài toán, ta có \(I\left( 0\,;\,0 & \,;\,-1 \right)\,,\,R=\sqrt{5}\,,\,A\left( a\,;\,b\,;\,0 \right)\), ta có
\(5\le {{a}^{2}}+{{b}^{2}}+1\le 10\Rightarrow 4\le {{a}^{2}}+{{b}^{2}}\le 9\)
Do đó:
\(\left\{ \begin{array}{l} a = 0\\ b = \pm 2 \end{array} \right.\\ \left\{ \begin{array}{l} b = 0\\ a = \pm 2 \end{array} \right.\\ \left\{ \begin{array}{l} a = \pm 2\\ b = \pm 2 \end{array} \right.\\ \left\{ \begin{array}{l} a = \pm 1\\ b = \pm 2 \end{array} \right.\\ \left\{ \begin{array}{l} b = \pm 1\\ a = \pm 2 \end{array} \right.\\ \left\{ \begin{array}{l} a = 0\\ b = \pm 3 \end{array} \right.\\ \left\{ \begin{array}{l} b = 0\\ a = \pm 3 \end{array} \right.\)
KL: có 20 điểm thỏa mãn bài toán.
.png)















