Cho hàm số \(y=f\left( x \right)\) có BBT như sau:
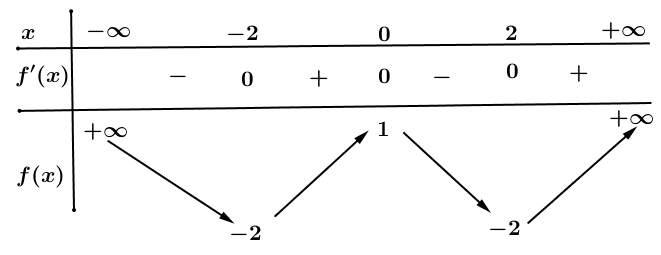
Có bao nhiêu giá trị nguyên dương \(m\) để phương trình \(3f\left( x \right)+2m=0\) có \(2\) nghiệm thực phân biệt?
Chính xác
Xem lời giải
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Chủ đề: Đề thi THPT QG
Môn: Toán
Lời giải:
Báo saiTa có \(3f\left( x \right)+2m=0\Leftrightarrow f\left( x \right)=-\frac{2m}{3}\)
Từ bảng biến thiên để phương trình trên có 2 nghiệm
\(\Leftrightarrow \left[ \begin{align} & -\frac{2m}{3}>1 \\ & -\frac{2m}{3}=-2 \\ \end{align} \right.\) \(\Leftrightarrow \left[ \begin{align} & m<-\frac{3}{2} \\ & m=3 \\ \end{align} \right.\)
Mà \(m\) nguyên dương suy ra \(m=3\). Vậy có \(1\) giá trị nguyên dương \(m\) thỏa mãn bài toán.
Chọn D
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề thi thử tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Trần Cao Vân
26/12/2024
627 lượt thi
0/50
Bắt đầu thi
ADMICRO
YOMEDIA
ZUNIA9











