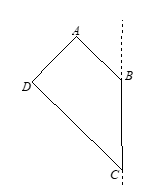
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có cạnh bằng \(a\). Gọi \(\alpha \) là góc giữa \(\left( AC{D}' \right)\) & \(\left( ABCD \right)\). Giá trị của \(\tan \alpha \) bằng?
Chính xác
Xem lời giải
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Chủ đề: Đề thi THPT QG
Môn: Toán
Lời giải:
Báo sai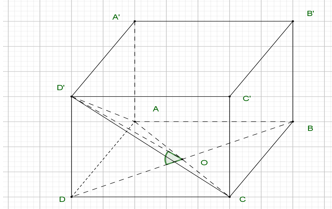
Gọi \(O\) là trung điểm của \(AC\).
Tam giác \(D'AC\)cân tại \(D'\Rightarrow DO\bot AC\).Do đó góc giữa \(\left( AC{D}' \right)\)
và \(\left( ABCD \right)\) là \(\widehat{D'OD}=\alpha \)\( \Rightarrow \tan \alpha \)\( =\frac{DD'}{DO}=\frac{a}{\frac{a\sqrt{2}}{2}}\)\( =\sqrt{2}.\)
Chọn A
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Sương Nguyệt Anh
26/12/2024
120 lượt thi
0/50
Bắt đầu thi
ADMICRO
YOMEDIA
ZUNIA9