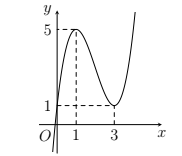
Hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) có đồ thị như hình:
.PNG)
Khẳng định nào là đúng?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐồ thị hàm số là đường đi lên từ \(-\infty \) nên \(a>0\).
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên \(d>0\).
Hàm số có hai điểm cực trị \({{x}_{1}},\,{{x}_{2}}\) thỏa mãn \(-1<{{x}_{1}}<0<1<{{x}_{2}}\) nên \({y}'=3a{{x}^{2}}+2bx+c\) có hai nghiệm \({{x}_{1}},\,{{x}_{2}}\) thỏa mãn \(-1<{{x}_{1}}<0<1<{{x}_{2}}\).
Suy ra: \(\left\{ \begin{align} & {{x}_{1}}+{{x}_{2}}=-\frac{2b}{3a}>0 \\ & {{x}_{1}}.{{x}_{2}}=\frac{c}{3a}<0 \\ \end{align} \right.\).
Kết hợp với \(a>0\), \(d>0\) ta được: \(a>0\), \(b<0\), \(c<0\), \(d>0\).
Chọn A
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Tân Phong
Câu hỏi liên quan
-
Cho HS \(y=f(x)\) có đạo hàm trên \(\mathbb{R}\), thỏa mãn \(f(2) \leq f(-2)=2020\). Hàm số \(y={f}'(x)\) có đồ thị như hình:
.PNG)
Hàm số \(g(x)=[2020-f(x)]^2\) nghịch biến trên khoảng?
-
Với các số thực dương \(a\), \(b\) bất kì, mệnh đề nào sai?
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\). Biết cạnh bên \(SA=2a\) và vuông góc với mp đáy. Tính thể tích của khối chóp \(S.ABCD\)?
-
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có cạnh bằng \(3\). Tính diện tích xung quanh \({{S}_{xq}}\) hình nón có đáy là đường tròn nội tiếp hình vuông \(ABCD\) và đỉnh là tâm hình vuông \({A}'{B}'{C}'{D}'\)?
-
Cho hình nón có chiều cao bằng \(8\,\text{cm}\), bán kính đáy bằng \(6\,\text{cm}\). Diện tích toàn phần Stp của hình nón đã cho bằng?
-
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có BBT như sau:
.PNG)
Phương trình \(f\left( x \right)=4\) có bao nhiêu nghiệm thực?
-
Thể tích của khối hình hộp chữ nhật có các kích thước lần lượt là \(a\); \(2a\); \(3a\) bằng?
-
Cho hàm số \(y=f(x)\) xác định trên \(\mathbb{R}\) và có bảng xét dấu sau:
Hàm số \(f(x)\) có bao nhiêu điểm cực trị?
-
Cho hàm số \(y=f\left( x \right)\). ĐTHS đạo hàm \(y={f}'\left( x \right)\) như hình vẽ bên. Đặt \(h\left( x \right)=3f\left( x \right)-{{x}^{3}}+3x\). Tìm mệnh đề đúng trong các mệnh đề sau?
-
Cho hàm số \(y=f\left( x \right)\) có BBT như sau:
Gọi \(M,\text{ }m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=f\left( 2\cos x+1 \right)\). Tính \(M+m\)?
-
Hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x+7\) đồng biến trên khoảng nào?
-
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(2a,\) cạnh bên bằng \(3a\). K/c từ \(A\) đến mặt phẳng \(\left( SCD \right)\) bằng?
-
Với \(a,\,b\) là 2 số thực dương tùy ý, biểu thức \({{\log }_{2022}}\left( 2022{{a}^{2}}b \right)\) bằng?
-
Cắt mặt cầu \(\left( S \right)\) bằng 1 mặt phẳng cách tâm một khoảng bằng 4 \(\text{cm}\) ta được 1 thiết diện là đường tròn có bán kính bằng \(3\)\(\text{cm}\). Bán kính của mặt cầu \(\left( S \right)\) là?
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), SA vuông góc với đáy và \(SA=a\sqrt{3}\). Góc giữa đt \(SD\) và mp \((ABCD)\) bằng?
-
Có tất cả bao nhiêu giao điểm của đồ thị hàm số \(y={{x}^{3}}+3x-3\) với trục \(Ox\)?
-
Có bao nhiêu số nguyên \(x\in \left[ -2022;2022 \right]\) thỏa mãn rằng \(\left( {{3}^{{{x}^{2}}}}-{{27}^{x}} \right)\sqrt{{{\log }_{2}}\left( 4x \right)-2}\ge 0\)?
-
Tính đạo hàm của hàm số sau \(y={{6}^{x}}\)?
-
Trong bốn hàm số được liệt kê ở bốn phương án \(\text{A, B, C, D}\) dưới đây, hàm số nào bên dưới có bảng biến thiên sau?
-
Cho cấp số cộng sau \(\left( {{u}_{n}} \right)\) có số hạng đầu \({{u}_{1}}=3\) và công sai \(d=2\). Giá trị của \({{u}_{7}}\) bằng?
