Cho số phức z thỏa mãn \(|z-3|=2|z|\) và \(\max |z-1+2 i|=a+b \sqrt{2}.\) Tính a+b
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\begin{array}{l} \text { Gọi } z=x+y i(x, y \in \mathbb{R}) \\ \text { Khi đó }|z-3|=2|z| \Leftrightarrow|(x-3)+y i|=2|x+y i| \Leftrightarrow \sqrt{(x-3)^{2}+y^{2}}=2 \sqrt{x^{2}+y^{2}} \\ \Leftrightarrow(x-3)^{2}+y^{2}=4\left(x^{2}+y^{2}\right) \Leftrightarrow 3 x^{2}+3 y^{2}+6 x-9=0 \end{array}\)
\(\Leftrightarrow x^{2}+y^{2}+2 x-3=0 \Leftrightarrow(x+1)^{2}+y^{2}=2^{2}\)
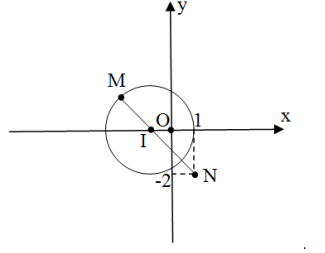
Suy ra tập hợp các điểm M biểu diễn z chính là đường tròn tâm \( I(-1 ; 0), R=2\) .
Ta có \(|z-1+2 i|=|z-(1-2 i)|=M N, N(1 ;-2)\).
Dựa vào hình vẽ nhận thấy MN lớn nhất khi đi qua tâm.
Khi đó \(M N=N I+I M=2 \sqrt{2}+R=2 \sqrt{2}+2 . \text { Suy ra } a=2, b=2\).
Do đó \(a+b=2+2=4\)