Sóng dừng trên một sợi dây đàn hồi OB mô tả như hình dưới. Điểm O trùng với gốc tọa độ trục tung. Lúc t = 0 hình ảnh của sợi dây là (1), sau thời gian nhỏ nhất ∆t và 3∆t kể từ lúc t = 0 thì hình ảnh của sợi dây lần lượt là (2) và (3). Tốc độ truyền sóng là 20 m/s và biên độ của bụng sóng là 4 cm. Sau thời gian 1/30 s kể từ lúc t = 0, tốc độ dao động của điểm M là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDựa vào đồ thị, ta có \(2\lambda =80\text{ cm}\Rightarrow \lambda =40\text{ cm}\text{.}\)
Chu kì chuyển động của sóng dừng: \(T=\frac{\lambda }{v}=\frac{40}{2000}=0,02\text{ s}\text{.}\)
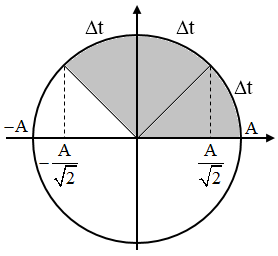
Dựa vào đề bài, ta có hình vẽ như bên.
+ Khoảng thời gian: \(\Delta t=\frac{T}{4}={{5.10}^{-3}}\text{ s}\text{.}\)
+ Biên độ dao động của điểm M là \({{A}_{M}}=\frac{A}{\sqrt{2}}=\frac{4}{\sqrt{2}}=2\sqrt{2}\text{ cm}\text{.}\)
Tại thời điểm t = 0, điểm M đang ở vị trí biên dương và đang chuẩn bị đi xuống nên \({{\varphi }_{M}}=0.\)
Phương trình vận tốc của M: \({{v}_{M}}=-\frac{2\pi }{T}.{{A}_{M}}.\sin \left( \frac{2\pi }{T}.t \right)=-200\pi \sqrt{2}.\sin 100\pi t\text{ (cm/s)}\text{.}\)
Vận tốc của điểm M tại thời điểm 1/30 s là
\({{v}_{M}}=-200\pi \sqrt{2}.\sin \left( 100\pi .\frac{1}{30} \right)=100\pi \sqrt{6}\text{ cm/s}\approx 7,7\text{ m/s}\text{.}\)
Câu hỏi liên quan
-
Một dây AB có đầu A cố định, đầu B tự do. Khi dây rung với tần số 80 Hz thì trên dây có sóng dừng và đếm được có 4 nút sóng kể cả nút sóng tại A. Biết tốc độ sóng trên dây là 4 m/s. Chiều dài dây là
-
Khi nói về sóng dừng trên một sợi dây đàn hồi, phát biểu nào sau đây sai?
-
Trên một sợi dây đàn hồi dài 1,6 m và hai đầu cố định đang có sóng dừng. Biết tần số của sóng là 20 Hz, tốc độ truyền sóng trên dây là 4 m/s. Số bụng sóng trên dây là
-
Một âm thoa được đặt phía trên miệng ống, cho âm thoa dao động với tần số 400 Hz. Chiều dài của cột khí trong ống có thể thay đổi bằng cách thay đổi mực nước trong ống. Ống được đổ đầy nước, sau đó cho nước chảy ra khỏi ống. Hai lần cộng hưởng gần nhau nhất xảy ra khi chiều dài của cột khí là 0,175m và 0,525m. Tốc độ truyền âm trong không khí bằng
-
Khi xảy ra hiện tượng sóng dừng trên, khoảng cách giữa hai nút sóng liên tiếp là
-
Sóng dừng ổn định trên sợi dây có chiều dài L = OB = 1,2 m với hai đầu O và B là hai nút sóng. Tại thời điểm t = 0, các điểm trên sợi dây có li độ cực đại và hình dạng sóng là đường (1), sau đó một khoảng thời gian ∆t và 5∆t các điểm trên sợi dây chưa đổi chiều chuyển động và hình dạng sóng tương ứng là đường (2) và (3). Tốc độ truyền sóng trên dây bằng 6 m/s, biên độ dao động là 2a = 1,2 cm. Tốc độ cực đại của điểm M là
-
Sóng truyền trên một sợi dây đàn hồi, hai điểm trên dây cách nhau những khoảng d= (k + ½) λ thì sẽ dao động:
-
Chọn câu sai về sự phản xạ sóng
-
Sóng dừng được hình thành bởi
-
Biểu thức sóng tổng hợp của sóng tới và sóng phản xạ tại một điểm M cách đầu cố định khoảng x cho bởi: \(u=2cos\left( \frac{\pi }{4}x+\frac{\pi }{2} \right)sin20\pi t\,\,~\left( cm \right).\) Trong đó x tính bằng cm và t tính bằng s. Các điểm nút cách đầu cố định khoảng
-
Để tạo sóng dừng trên dây người ta điều chỉnh tần số f của nguồn. f = 42 Hz và f = 54 Hz là hai giá trị tần số liên tiếp mà trên dây có sóng dừng. Giá trị nào sau đây của f thì trên dây không thể có sóng dừng?
-
Trên 1 sợi dây đàn hồi đang có sóng dừng. Khoảng cách từ một nút đến một bụng kề nó bằng
-
Một sợi dây AB dài 4,5m có đầu dưới A để tự do, đầu trên B găn với một cần rung với tần số f có thể thay đổi được. Ban đầu trên dây có sóng dừng với đầu A bụng đầu B nút. Khi tần số f tăng thêm 3 Hz thì số nút trên dây tăng thêm 18 nút và A vẫn là bụng B vẫn là nút. Tính tốc độ truyền sóng trên sợi dây.
-
Một sóng ngang truyền trên bề mặt với tân số f=10Hz. Tại một thời điểm nào đó một phần mặt cắt của nước có hình dạng như hình vẽ. Trong đó khoảng cách từ vị trí cân bằng của A đến vị trí cân bằng của D là 60cm và điểm C đang đi xuống qua vị trí cân bằng. Chiều truyền sóng và tốc độ truyền sóng là:
.PNG)
-
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, A là một điểm nút, B là điểm bụng gần A nhất với AB = 18 cm, M là một điểm trên dây cách B một khoảng 12 cm. Biết rằng trong một chu kỳ sóng, khoảng thời gian mà độ lớn vận tốc dao động của phần tử B nhỏ hơn vận tốc cực đại của phần tử M là 0,1s. Tốc độ truyền sóng trên dây là
-
Một sợi dây đàn hồi AB có chiều dài 15cm và hai đầu cố định. Khi chưa có sóng thì M và N là hai điểm trên dây với với AM = 4cm và BN = 8 cm. Khi xuất hiện sóng dừng, quan sát thấy trên dây có 5 bụng sóng và biên độ của bụng là 1cm. Tỉ số giữa khoảng cách lớn nhất và khoảng cách nhỏ nhất giữa hai điểm M, N xấp xỉ bằng
-
Trong sóng dừng trên dây, hiệu số pha của hai điểm trên dây nằm đối xứng qua một nút bằng:
-
Trên một sợi dây dài 90cm có sóng dừng. Kế cả hai nút ở hai đầu dây thì trên dây có 10 nút sóng. Biết tần số của sóng truyền trên dây là 200Hz. Sóng truyền trên dây có tốc độ là
-
Phát biểu nào sau đây là đúng? Khi có sóng dừng trên dây đàn hồi thì
-
Khi sóng cơ truyền trên sợi đây bị phản xạ tại đầu cố định
