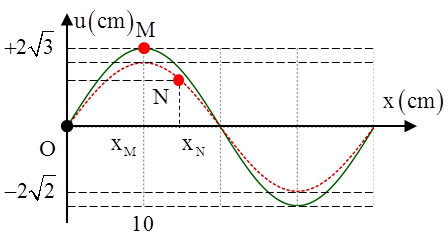
Sóng dừng ổn định trên sợi dây có chiều dài L = OB = 1,2 m với hai đầu O và B là hai nút sóng. Tại thời điểm t = 0, các điểm trên sợi dây có li độ cực đại và hình dạng sóng là đường (1), sau đó một khoảng thời gian ∆t và 5∆t các điểm trên sợi dây chưa đổi chiều chuyển động và hình dạng sóng tương ứng là đường (2) và (3). Tốc độ truyền sóng trên dây bằng 6 m/s, biên độ dao động là 2a = 1,2 cm. Tốc độ cực đại của điểm M là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa xét chuyển động của điểm bụng gần O nhất. Ta có hình vẽ như sau:
+ Trong thời gian 3Dt, ta có:\(\omega \Delta t+\omega 2\Delta t=\frac{\pi }{2}\Rightarrow \omega \Delta t=\frac{\pi }{6}.\)
=> trong thời gian điểm bụng di chuyển từ vị trí biên dương đến vị trí có li độ \(u=\sqrt{3}a.\)
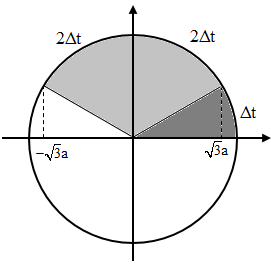
Dựa vào hình ảnh đề bài, ta có:
\(\lambda =\frac{2.OB}{5}=0,48\text{ }m\Rightarrow \omega =\frac{2\pi }{T}=\frac{2\pi .v}{\lambda }=25\pi \text{ rad/s}\text{.}\)
Biên độ cực đại của điểm M là \({{A}_{M}}=a\sqrt{3}=0,6\sqrt{3}\text{ cm}.\)
Vận tốc cực đại của điểm M: \({{v}_{M\max }}=\omega .{{A}_{M}}\approx 81,62\text{ cm/s}\text{.}\)