Biết số phức z thõa mãn \(|z-1| \leq 1 \text { và } z-\bar{z}\) có phần ảo không âm. Phần mặt phẳng biểu diễn số phức z có diện tích là:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai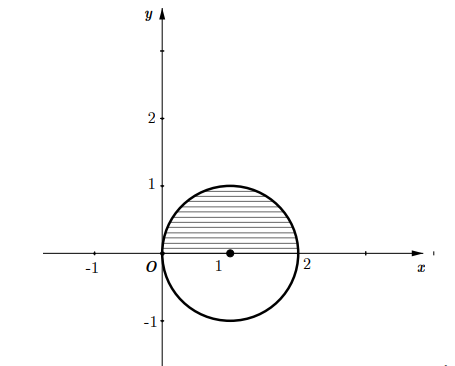
Đặt \(z=x+y i \Rightarrow \bar{z}=x+y i\)
Khi đó ta có:
\(\begin{array}{l} |z-1| \leq 1 \Leftrightarrow|(x+y i)-1| \leq 1 \\ \Leftrightarrow|(x-1)+y i| \leq 1 \Leftrightarrow(x-1)^{2}+y^{2} \leq 1(1) \end{array}\)
\(z-\bar{z}=(x+y i)-(x-y i)=2 y i\) có phần ảo không âm suy ra \(y \geq 0(2)\)
Từ (1) và (2) ta suy ra phần mặt phẳng biểu diễn số phức z là nửa hình tròn tâm I(1 ; 0) bán kính r =1, diện tích của nó bằng \(\frac{1}{2} \cdot r^{2} \pi=\frac{\pi}{2}(\mathrm{đvdt})\)
ADMICRO
YOMEDIA
ZUNIA9











