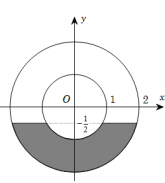
Cho các số phức thỏa mãn điều kiện và . Giá trị của biểu thức bằng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
ZUNIA9