Cho các số phức z thỏa mãn \(|z-3+4 i|=2\) và cho số phức \(w=2 z+1-i\) . Khi đó |w| có giá trị lớn nhất bằng bao nhiêu?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\begin{aligned} &\text { Đặt } z=x+y i \text { với } x, y \in \mathbb{R} \text { . }\\ &\text { Khi đó }|z-3+4 i|=2 \Leftrightarrow(x-3)^{2}+(y+4)^{2}=4\\ &\text { Goi } M \text { là điểm biểu diễn hình học của số phức } z \text { ta có } M \in(I ; 2) \text { với } I(3 ;-4) \text { . }\\ &\mathrm{w}=2 z+1-i=2 x+1+(2 y-1) i \Rightarrow|\mathrm{w}|=\sqrt{(2 x+1)^{2}+(2 y-1)^{2}}=\sqrt{4\left[\left(x+\frac{1}{2}\right)^{2}+\left(y-\frac{1}{2}\right)^{2}\right]} \end{aligned}\)
\(\begin{aligned} &\text { Gọi } A\left(-\frac{1}{2} ; \frac{1}{2}\right) \text { suy ra }|\mathrm{w}|=\sqrt{4\left[\left(x+\frac{1}{2}\right)^{2}+\left(y-\frac{1}{2}\right)^{2}\right]}=2 A M\\ &\text { Dễ thấy } A I=\sqrt{\left(3+\frac{1}{2}\right)^{2}+\left(-4-\frac{1}{2}\right)^{2}}=\frac{\sqrt{130}}{2}>2 \text { nên } A \text { nằm ngoài }(I ; 2) \text { . } \end{aligned}\)
Kẻ đường thẳng AI cắt đường tròn (I;2) tại BC, như hình vẽ.
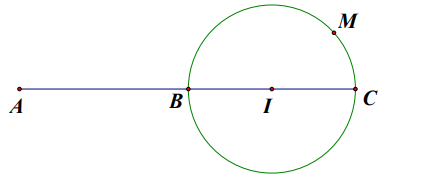
Có \(A M \leq A C \text { nên } A M_{\max }=A C\).
Dấu “=” xảy ra khi và chỉ khi \(M \equiv C \). Khi đó \(A C=A I+I C=\frac{\sqrt{130}}{2}+2=\frac{\sqrt{130}+4}{2}\)
\(\text { Vậy }|\mathrm{w}|_{\max }=2 A C=\sqrt{130}+4 \text { . }\)
