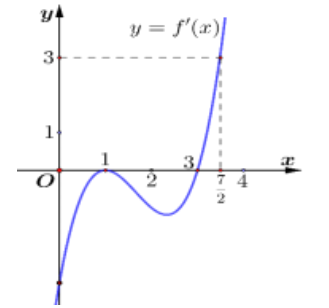
Cho hàm số f(x). Biết hàm số y = f'(x) có đồ thị như hình bên. Trên đoạn \({\rm{[}} – 4;3]\), hàm số \(g(x) = 2f(x) + {(1 – x)^2}\) đạt giá trị nhỏ nhất tại điểm.

Câu hỏi liên quan

• Cho hàm số \(y = \left| {{x^2} + 2x + a – 4} \right|\). Tìm a để giá trị lớn nhất của hàm số trên đoạn \(\left[ { – 2;1} \right]\) đạt giá trị nhỏ nhất?

• Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f’\left( x \right)\) như hình vẽ

  

  Đặt \(g\left( x \right) = \frac{1}{3}{x^3} – x – f\left( x \right) + 2020\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { – \sqrt 3 ;\,\sqrt 3 } \right]\). Hãy tính M + m.

• Giá trị nhỏ nhất của hàm số \(y=e^{x}\left(x^{2}-3\right)\) trên đoạn [-2;2] là
   

ZUNIA12

• Giá trị lớn nhất của hàm số \(y = \left\{ \begin{array}{l}
   - {x^2} + 3,\;\,\,\,\,\, - 2 \le x \le 0\\
  3 - x,\;\,\,\,\,0 < x \le 3\\
  x - 3,\;\,\,\,\,3 < x \le 7
  \end{array} \right.\) có đồ thị như hình bên là 

  

• Cho hàm số \(f(x)=\sin ^{3} x-3 \sin x+2 .\) Gọi và lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho.
  Khi đó là \(M+2 m\) là?

• Cho một tấm nhôm hình vuông cạnh 18 cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x cm , rồi gấp tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.

  

• Tìm giá trị nhỏ nhất của hàm số \(y=\frac{x^2-5}{x+3}\)trên đoạn [0;2]

   

• Giá trị lớn nhất của hàm số y=x³ −3x+5 trên đoạn \( \left[ {0;\frac{3}{2}} \right]\)

• Giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} – 8{x^2} + 16x – 9\) trên đoạn \(\left[ {1;\,3} \right]\) là

• Tìm giá trị nhỏ nhất của hàm số \(y=\frac{x^2-4x}{2x+1}\)trên đoạn [0;3]

• Giá trị lớn nhất của hàm số \(f(x)=\frac{\ln x}{x}\) trên đoạn [1;3] là:

• Cho hàm số \(y=\left|x^{3}-3 x^{2}+m\right|\)(với m là tham số thực). Hỏi \(\max _{[1 ; 2]} y\) có giá trị nhỏ nhất bằng bao nhiêu?

• \(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{3x - 11}}{{x + 2}}\text{ trên đoạn } \left[ {1;5} \right]\)

• Cho hai số thực x y , thay đổi thỏa mãn điều kiện \(x^{2}+y^{2}=2\) . Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức \(P=2\left(x^{3}+y^{3}\right)-3 x y\) . Giá trị của M + n bằng: 

• Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=\frac{x-1}{2x+1}\)trên đoạn [1;3] là:

• Cho hàm số \(y = \left| {{x^4} - 4{x^3} + 4{x^2} + a} \right|\). Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M ≤ 2m?

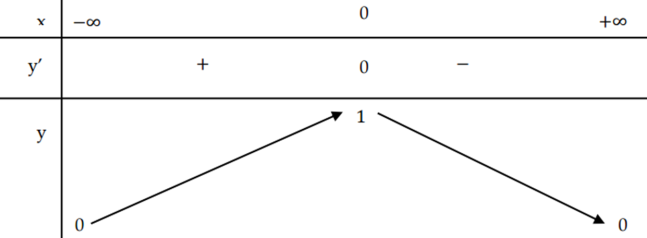
• Cho hàm số y=f(x) xác định, liên tục trên và có bảng biến thiên như sau: 

  

  Giá trị lớn nhất của hàm số y=f(x) trên đoạn [ 0; 2] bằng:

• Giá trị lớn nhất của hàm số \(y = \frac{{x + 5}}{{x – 7}}\) trên đoạn \(\left[ {8;12} \right]\) là

• Giá trị nhỏ nhất của hàm số \(y=2x+1+\frac{1}{2x+1}\)trên đoạn [1; 2] bằng

   

• \(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - 2x - 5}}{{x + 3}}\text{ trên đoạn } \left[ { - 2;1} \right]\)