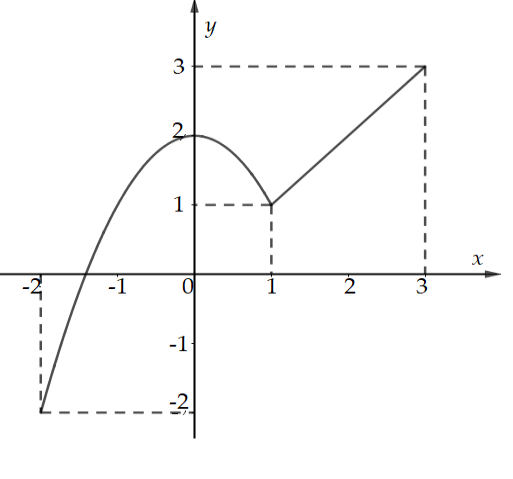Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Đồ thị của hàm số \(y = f’\left( x \right)\) như hình vẽ dưới đây.
.jpg.png)
Xét hàm số \(g\left( x \right) = 2f\left( x \right) – {\left( {x + 1} \right)^2}\). Mệnh đề nào sau đây là đúng?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(g’\left( x \right) = 2f’\left( x \right) – 2\left( {x + 1} \right) = 0 \Leftrightarrow f’\left( x \right) = x + 1\,\left( * \right)\)
.jpg.png)
Dựa vào đồ thị hàm số \(y = f’\left( x \right)\) ta thấy đường thẳng y = x + 1 cắt đồ thị hàm số \(y = f’\left( x \right)\) tại ba điểm lần lượt có hoành độ là: \( – 3\,;\,1\,;\,3\). Do đó phương trình \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}x = – 3\\x = 1\\x = 3\end{array} \right.\)
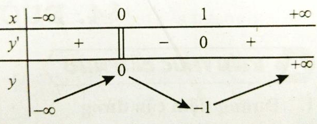
Bảng biến thiên của hàm số \(y = g\left( x \right)\)
.png)
Vậy \(\mathop {{\rm{max}}}\limits_{\left[ { – 3\,;\,3} \right]} g\left( x \right) = g\left( 1 \right)\,\).
.jpg.png)