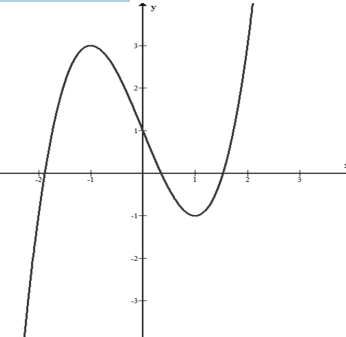
Cho hàm số \(f(x)=x^{4}-4 x^{2}+3\) có đồ thị là đường cong trong hình bên. Hỏi phương trình \(\left(x^{4}-4 x^{2}+3\right)^{4}-4\left(x^{4}-4 x^{2}+3\right)^{2}+3=0\) có bao nhiêu nghiệm thực phân biệt ?
8
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=x^{4}-2 x^{2}+3\)
Khi đó ta có phương trình: \(t^{4}-4 t^{2}+3=0\,\,\,(2)\)
Nghiệm của phương trình (2) là hoành độ giao điểm của đồ thị hàm số và trục hoành.
Dựa vào đồ thị ta thấy: phương trình (2) có 4 nghiệm
\(\left[\begin{array}{l} t=-\sqrt{3} \\ t=-1 \\ t=1 \\ t=\sqrt{3} \end{array} \Rightarrow\left[\begin{array}{l} x^{4}-2 x^{2}+3=-\sqrt{3} \\ x^{4}-2 x^{2}+3=-1 \\ x^{4}-2 x^{2}+3=1 \\ x^{4}-2 x^{2}+3=\sqrt{3} \end{array}\right.\right. \Leftrightarrow \left[ \begin{array}{l} f\left( x \right) = - \sqrt 3 \,\, \,\,\,\,\,(3) \\ f\left( x \right) = - 1\,\,\,\,\,\,\,\,\,\,\,\,(4)\\ f\left( x \right) = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(5)\\ f\left( x \right) = \sqrt 3 \,\,\,\,\,\,\,\,\,\,(6) \end{array} \right.\)
Dựa vào đồ thị hàm số suy ra:
(3) vô nghiệm.
(4) có hai nghiệm.
(5) có 4 nghiệm.
(6) có 4 nghiệm.
vậy phương tình đã cho có 10 nghiệm
Câu hỏi liên quan
-
Hai điểm A,B thuộc hai nhánh của đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaaiodacqGHRaWkdaWcaaqaaiaaiEdaaeaacaWG4bGaeyOeI0Ia % aG4maaaaaaa!3D0F! y = 3 + \frac{7}{{x - 3}}\). Khi đó độ dài đoạn thẳng AB ngắn nhất bằng bao nhiêu?
-
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình: \(-x^{3}+3 m x-2<-\frac{1}{x^{3}}\) nghiệm đúng \(\forall x \geq 1 ?\)
-
Đồ thị hàm số \(y = {x^4} – {x^2} + 1\) cắt trục tung tại điểm có tung độ bằng
-
Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4}-2{x^2}\) tại điểm có hoành độ x = - 2 là:
-
Đồ thị sau đây là của hàm số nào?
-
Cho hàm số \(y = {x^4} – \left( {2m – 1} \right){x^2} + 2m\) có đồ thị (C). Tất cả các giá trị của tham số m để đường thẳng d: y = 2 cắt đồ thị (C) tại bốn điểm phân biệt đều có hoành độ nhỏ hơn 3 là
-
Tung độ giao điểm của đồ thị các hàm số y = x3 – 3x2 + 2, y = - 2x + 8 là:
-
Cho hàm số y = x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y = 0 là
-
Tất cả giá trị của tham số m để đồ thị \((C): y=x^{4}-2 x^{2}-3\) cắt đường thẳng d: y=m tại bốn điểm phân biệt là
-
Cho các phát biểu sau:
I. Đồ thị hàm số có y = x4 – x + 2 có trục đối xứng là Oy.
II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x0 thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x0,f(x0)) song song với trục hoành.
III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b).
IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x0 thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x0) và đồng biến trên khoảng (x0;b).
Các phát biểu đúng là:
-
Giá trị của m để phương trình \(x+\sqrt{2 x^{2}+1}=m\) có nghiệm là:
-
Đồ thị hình bên là của hàm số nào? Chọn một khẳng định ĐÚNG.
-
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(\sqrt{x^{2}+m x+2}=2 x+1\) có hai nghiệm thực?
-
Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số \(y\; = \;\frac{x}{{\left| {x\; - \;1} \right|}}\) ?
-
Có bao nhiêu điểm thuộc đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaaI % ZaGaamiEaiabgUcaRiaaiodaaaa!3F1C! y = - {x^3} - 3x + 3\) cách giao điểm của đồ thị hàm số với trục tung một khoảng bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaaca % aIXaGaaG4naaWcbeaaaaa!378B! \sqrt {17} \)?
-
Cho hàm số \(y = \sqrt {2 - {x^2}} .\) Gọi M và mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Khi đó M − 2m bằng
-
Đồ thị sau đây là của hàm số nào?
-
Hàm số \(y=(x-2)(x^2-1)\) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số \(y=|(x-2).|x-1|.(x+1)|\)
.png)
-
Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên?
-
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 5\) là đường thẳng
