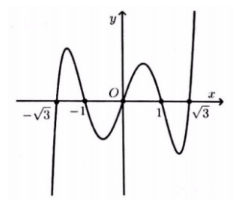
Cho hàm số \(y=f^{\prime}(x-1)\) có đồ thị như hình vẽ.
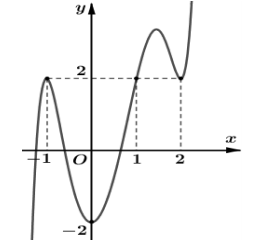
Hàm số \(y=\pi^{2 f(x)-4 x}\) đạt cực tiểu tại điểm nào?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(y^{\prime}=0 \Leftrightarrow 2 f^{\prime}(x)-4=0 \Leftrightarrow f^{\prime}(x)=2\)
Đồ thị hàm số \(y=f^{\prime}(x)\) nhận được từ việc tịnh tiến đồ thị hàm số \(y=f^{\prime}(x-1)\)sang trái 1 đơn vị

nên \(f^{\prime}(x)=2 \Leftrightarrow\left[\begin{array}{l} x=-2 \\ x=0 \\ x=1 \end{array}\right.\)
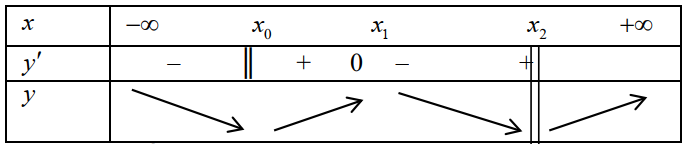
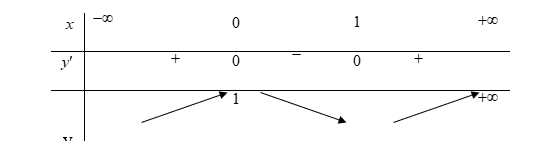
Do x =-2 và x =1 là nghiệm bội chẵn nên ta có bảng biến thiên sau:

Từ bảng biến thiên ta có hàm số đạt cực tiểu tại x=0 .
ADMICRO
YOMEDIA
ZUNIA9