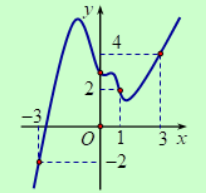
Cho hàm số \(y=f(x)\) có đồ thị của hàm số \(y=f'(x)\)như hình vẽ bên
Hàm số \(y=39 f(x)-8 x^{3}+45 x^{2}-276 x+1\) đồng biến trên khoảng nào dưới đây?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTa có \(y^{\prime}=39 f^{\prime}(x)-24 x^{2}+90 x-276\)
Hàm số đã cho đồng biến \(\Leftrightarrow y^{\prime} \geq 0 \Leftrightarrow f^{\prime}(x) \geq \frac{24 x^{2}-90 x+276}{39}\)
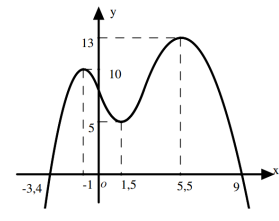
Gọi (P) là đồ thị hàm số \(y=\frac{24 x^{2}-90 x+276}{39}\)Ta có đồ thị hàm số f '(x) và (P) được thể hiện trong hình sau:

Từ đồ thị trên ta thấy đồ thị hàm số f'(x) nằm phía trên parabol (P) trên khoảng \(\left(-1 ; \frac{11}{2}\right)\)
Vậy \(f^{\prime}(x) \geq \frac{24 x^{2}-90 x+276}{39} \Leftrightarrow x \in\left(-1 ; \frac{11}{2}\right)\)
ADMICRO
YOMEDIA
ZUNIA9