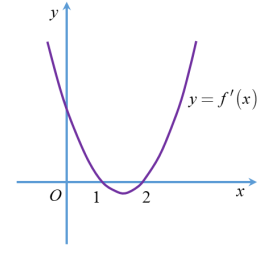
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = {x^3} – 3{x^2} + \left( {1 – m} \right)x\) đồng biến trên khoảng \(\left( {2; + \infty } \right)\) là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(y’ = 3{x^2} – 6x + 1 – m\)
Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right) \Leftrightarrow y’ \ge 0, \forall x \in \left( {2; + \infty } \right)\)
\( \Leftrightarrow 3{x^2} – 6x + 1 – m \ge 0, \Leftrightarrow \frac{{\left| {2P + P} \right|}}{{\sqrt {{{\left( {2P} \right)}^2} + {{\left( {P – 4} \right)}^2}} }} \le 1 \Leftrightarrow 3\left| P \right| \le \sqrt {5{P^2} – 8P + 16} \)
\( \Leftrightarrow 3{x^2} – 6x + 1 \ge m, \Leftrightarrow \frac{{\left| {2P + P} \right|}}{{\sqrt {{{\left( {2P} \right)}^2} + {{\left( {P – 4} \right)}^2}} }} \le 1 \Leftrightarrow 3\left| P \right| \le \sqrt {5{P^2} – 8P + 16} \Leftrightarrow m \le \mathop {\min }\limits_{\left( {2; + \infty } \right)} g\left( x \right)\)
Xét hàm số \(g\left( x \right) = 3{x^2} – 6x + 1\) với \( \Leftrightarrow \frac{{\left| {2P + P} \right|}}{{\sqrt {{{\left( {2P} \right)}^2} + {{\left( {P – 4} \right)}^2}} }} \le 1 \Leftrightarrow 3\left| P \right| \le \sqrt {5{P^2} – 8P + 16} \).
\(g’\left( x \right) = 6x – 6; g’\left( x \right) > 0, \Leftrightarrow \frac{{\left| {2P + P} \right|}}{{\sqrt {{{\left( {2P} \right)}^2} + {{\left( {P – 4} \right)}^2}} }} \le 1 \Leftrightarrow 3\left| P \right| \le \sqrt {5{P^2} – 8P + 16} \).
Bảng biến thiên \(g\left( x \right)\):
.png)
Vậy \(m \le 1\)
Câu hỏi liên quan
-
Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 ngàn đồng một ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 ngàn đồng thì có thêm 2 phòng trống. Giám đốc phải chọn giá phòng mới là bao nhiêu để thu nhập của khách sạn trong ngày là lớn nhất.
-
Thể tích khối lăng trụ có diện tích đáy bằng \(3{a^2}\), chiều cao bằng a là
-
Hàm số \(y = \frac{1}{3}{x^3} + {x^2} - x\) nghịch biến trên các khoảng:
-
Tìm tham số m để hàm số \(f(x)=-\frac{x^{3}}{3}+(m-1) x^{2}+(m+3) x\) đồng biến trên khoảng (0;3)
-
Tìm các giá trị của tham số m sao cho hàm số \(y=\frac{x+1}{x+m}\) nghịch biến trên khoảng \((2 ;+\infty) .\)
-
Cho hàm số đa thức f (x) có đạo hàm tràm trên R . Biết f(0)=0 và đồ thị hàm số \(y=f^{\prime}(x)\) như hình sau.
Hàm số \(g(x)=\left|4 f(x)+x^{2}\right| \) đồng biến trên khoảng nào dưới đây -
Cho hàm số y = - x3 + 6x2 – 4. Mệnh đề nào dưới đây sai?
-
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaaIZaGaamiE % amaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiMdacaWG4bGaey4kaS % IaaGymaaaa!41CD! y = {x^3} - 3{x^2} - 9x + 1\) đồng biến trên khoảng nào trong những khoảng sau?
-
Tổng các giá trị nguyên của \(m \in[-25 ; 25]\) để hàm số \(y=\frac{(2 m+1) \tan x+1}{\tan x+m}\) đồng biến trên khoảng \(\left(0 ; \frac{\pi}{2}\right)\) là
-
Có bao nhiêu số nguyên \(m \in(-2020 ; 2020)\) để hàm số \(y=\frac{\cos x+1}{10 \cos x+m}\) đồng biến trên khoảng \(\left(0 ; \frac{\pi}{2}\right) ?\)
-
Cho hàm số \(y=f(x)=x^{3}+m x^{2}+2 x+3 \text { . }\)Tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên R là?
-
Hàm số \(y = - {x^3} - 2{x^2} + 3x\) nghịch biến trên khoảng nào sau đây?
-
Hàm số \(y = 2(x - 3)⁴ + 1\) đồng biến trong khoảng nào sau đây ?
-
Hàm số \(y=f(x)=x^4-12x^3\) nghịch biến trên
-
Gọi S là tập hợp các giá trị nào của tham số m để hàm số \(y=\frac{(m+1) x+2 m+2}{x+m}\) nghịch biến trên khoảng \((-1 ;+\infty)\). Khi đó S là tập con của tập nào sau đây?
-
Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\). Chọn khẳng định đúng
-
Cho hàm số y=f(x) có đạo hàm liên tục trên \(\mathbb{R}\) . Đồ thị hàm số y=f'(x) như hình vẽ
Hàm số \(g(x)=f(-2 x+1)+(x+1)(-2 x+4)\) đồng biến trên khoảng nào dưới đây -
Tìm tham số m để hàm số \(y=\frac{1}{3}(m-1) x^{3}+m x^{2}+(3 m-2) x\) là hàm đồng biến trên tập xác định của nó?
-
Hàm số \(y = {x^3} - 5{x^2} + 5\) đồng biến trên khoảng nào sau đây?
-
Hàm số \(y = {x^3} - 2{x^2} + x - 1\) đồng biến trên các khoảng:
