Cho hàm số \(y=\frac{x}{2}+\sin ^{2} x, x \in[0 ; \pi]\) . Hỏi hàm số đồng biến trên các khoảng nào?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(\mathrm{T} \mathrm{XD}: \mathrm{Đ}=\mathbb{R}\)
\(y^{\prime}=\frac{1}{2}+\sin 2 x\)
\(y^{\prime}=0 \Leftrightarrow \sin 2 x=-\frac{1}{2} \Leftrightarrow\left[\begin{array}{l}
x=-\frac{\pi}{12}+k \pi \\
x=\frac{7 \pi}{12}+k \pi
\end{array},(k \in \mathbb{Z})\right.\)
Do \(x \in[0 ; \pi]\) nên \(x=\frac{7 \pi}{12} \text { và } x=\frac{11 \pi}{12}\) thỏa điều kiện.
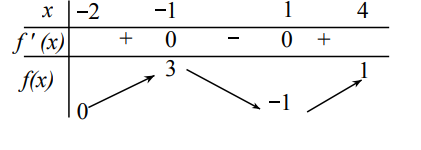
Bảng xét dấu
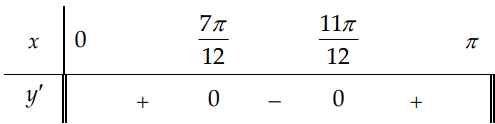
Hàm số đồng biến trên \(\left(0 ; \frac{7 \pi}{12}\right) \text { và }\left(\frac{11 \pi}{12} ; \pi\right)\)
ADMICRO
YOMEDIA
ZUNIA9
.PNG)











