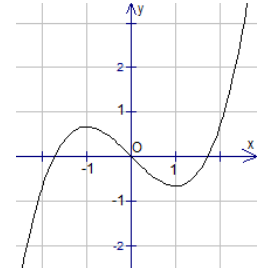
Cho hàm số y=f(x) có đạo hàm cấp 2 trên , hàm số \(y=f^{\prime}(x)\) có đồ thị như hình vẽ bên 

Giá trị lớn nhất của hàm số \(y=f\left(\frac{\sin x+\sqrt{3} \cos x}{2}\right) \text { trên đoạn }\left[-\frac{5 \pi}{6} ; \frac{\pi}{6}\right]\) bằng:

Câu hỏi liên quan

• Giá trị nhỏ nhất của hàm số \(y = x + \frac{9}{x}\) trên đoạn \(\left[ {2;\,4} \right]\) là:

• Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số \(\begin{equation} y=\left|\frac{x-m^{2}-m}{x+2}\right| \end{equation}\) thỏa \(\begin{equation} \max _{[1 ; 2]} y=1 \end{equation}\). Tích các phần tử của S bằng 

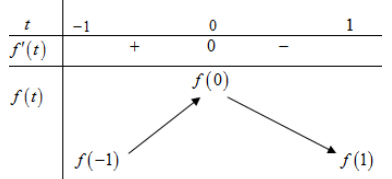
• Giá trị lớn nhất của hàm số \(f(x)=x^{3}-8 x^{2}+16 x-9\) trên đoạn [1;3] là:

ZUNIA12

• Giá trị nhỏ nhất của hàm số \(y=e^{x}\left(x^{2}-3\right)\) trên đoạn [-2;2]

• Cho hàm số y=f(x) có bảng biến thiên như sau: 

  

  Khẳng định nào sau đây đúng?

• Giá trị lớn nhất của hàm số \(y=2 \sin x-\frac{4}{3} \sin ^{3} x \text { trên }[0 ; \pi]\)  là:
   

• \(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{x - 11}}{{x + 2}}\text{ trên đoạn } \left[ { - 1;3} \right]\)

• Giá trị nhỏ nhất của hàm số y= 2sin⁴x+ cos²x+ 3 bằng

• Gọi A, B là giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = \frac{{x + {m^2} + m}}{{x – 1}}\) trên đoạn \(\left[ {2;3} \right]\). Tìm tất cả các giá trị thực của tham số m để \(A + B = \frac{{13}}{2}\).

• Giá trị lớn nhất của hàm số \(f\left( x \right) =  - {x^2} + 4\) là:

• Giá trị nhỏ nhất của hàm số \(y=3 \cos 2 x-4 \sin x\) là?

• Cho hàm số \(y = – {x^3} + 3{x^2} + 2\).Gọi M,n lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên \(\left[ {0;3} \right]\).Tính \(\left( {M + n} \right)\).

• Tìm giá trị nhỏ nhất của hàm số \(y=\frac{x^2-5}{x+3}\)trên đoạn [0;2]

   

• Hàm số \(f(x)=\frac{1}{\sin x}\) trên đoạn \(\left[\frac{\pi}{3} ; \frac{5 \pi}{6}\right]\) có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó M – m bằng
   

• Cho hàm số y = f(x) có đạo hàm cấp hai trên \(\mathbb{R}\). Biết f'(0) = 3,f'(2) = – 2018 và bảng xét dấu của f”(x) như sau:

  

  Hàm số y = f(x + 2017) + 2018x đạt giá trị nhỏ nhất tại điểm \({x_0}\) thuộc khoảng nào sau đây?

• Hàm số \(y=4 \sqrt{x^{2}-2 x+3}+2 x-x^{2}\) đạt giá trị lớn nhất tại hai giá trị \(x_{1}, x_{2}\) . Tính \(x_{1}. x_{2}\)

• Một chất điểm chuyển động theo quy luật \(S=6 t^{2}-t^{3}\) vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất tại thời điểm t (s) bằng

• Giá trị lớn nhất của hàm số \(f(x)=\frac{x^{2}+3 x-1}{x-2}\) trên đoạn [-2;0] là:

• Tìm giá trị lớn nhất (max) và giá trị nhỏ nhất (min) của hàm số \(y = x + \frac{1}{x}\) trên đoạn \(\left[ {\frac{3}{2};\,3} \right]\).

• Hàm số \(y=\cos ^{2} x-2 \cos x-1\) có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn \([0 ; \pi]\)lần lượt bằng \(y_{1} ; y_{2}\) . Khi đó tích \(y_{1} . y_{2}\) có giá trị bằng: