Cho hàm số có đồ thị C. Gọi M là một điểm bất kì trên C. Tiếp tuyến của C tại M cắt các đường tiệm cận của C tại A và B . Gọi I là giao điểm của các đường tiệm cận của C . Tính diện tích của tam giác IAB.
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTập xác định D = R\ { 1}.
Đạo hàm
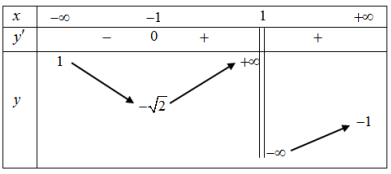
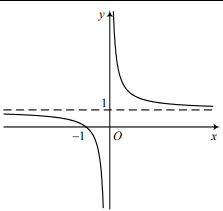
Đồ thị hàm số C có tiệm cận đứng là x = 1 và tiệm cận ngang y = 2 nên I (1 ;2 ) là giao của 2 đường tiệm cận.
Gọi
Tiếp tuyến ∆ của C tại M có phương trình là :
∆ cắt TCĐ tại và cắt TCN tại B(2x0-1 ; 2) .
Ta có
Do đó,
ADMICRO
YOMEDIA
ZUNIA9