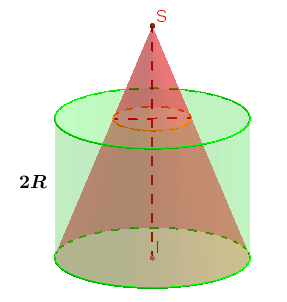
Cho hình cầu tâm O, đường kính 2R và hình trụ tròn xoay nội tiếp trong hình cầu. Hãy tìm kích thước của hình trụ khi nó có thể tích đạt giá trị lớn nhất.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi h và r là chiều cao và bán kính đáy của hình trụ. Bài toán quy về việc tính h và r phụ thuộc theo R khi hình chữ nhật ABCD nội tiếp trong hình tròn (O, R) thay đổi về \(V=\pi {{r}^{2}}h\)đạt giá trị lớn nhất
.png)
.png)
Ta có: \(A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\Leftrightarrow 4{{R}^{2}}=4{{r}^{2}}+{{h}^{2}}\)
\(\begin{align} & V=\pi \left( {{R}^{2}}-\frac{1}{4}{{h}^{2}} \right)h=\pi \left( -\frac{1}{4}{{h}^{3}}+{{R}^{2}}h \right)\,\,\,\,\,\left( 0<h<2r \right)="" \\="" &="" v'="\pi" \left(="" -\frac{3}{4}{{h}^{2}}+{{r}^{2}}="" \right)\,\leftrightarrow="" h="\pm" \frac{2r}{\sqrt{3}}="" \end{align}\)
.png)
Vậy \(V={{V}_{\text{max}}}=\frac{4}{9}\pi {{R}^{3}}\sqrt{3}\Leftrightarrow h=\frac{2R}{\sqrt{3}}\)
Lúc đó \({{r}^{2}}={{R}^{2}}-\frac{1}{4}.\frac{4{{R}^{2}}}{3}=\frac{2{{R}^{2}}}{3}\Rightarrow r=\frac{R\sqrt{6}}{3}\).
Câu hỏi liên quan
-
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a . Tính diện tích toàn phần của hình trụ đã cho.
-
Cho hình chữ nhật (ABCD ), khi quay hình chữ nhật quanh cạnh (AB ) thì (CD ) được gọi là:
-
Hình ABCD khi quay quanh BC thì tạo ra:
-
Cho hình chữ nhật ABCD có AC = 2AD = 2a. Quay quanh trục AB đường gấp khúc ADCB ta được hình trụ có diện tích xung quanh là:
-
Tính diện tích toàn phần của hình trụ có đường cao bằng 2 và đường kính đáy bằng 8.
-
Cho tam giác AOB vuông tại O. Quay tam giác quanh cạnh OA ta được hình nón có đường sinh và đường cao lần lượt là:
-
Thể tích khối trụ có bán kính (r = 4cm ) và chiều cao (h = 5cm ) là:
-
Cho hình nón có các kích thước (r = 1;h = 2 ) với (r,h ) lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:
-
Cho đường tròn tâm O bán kính r′. Xét hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, S và A cố định, SA=h cho trước và có đáy ABCD là một tứ giác tùy ý nội tiếp đường tròn đã cho, trong đó các đường chéo AC và BD vuông góc với nhau. Hỏi đáy ABCD là hình gì để thể tích hình chóp đạt giá trị lớn nhất?
-
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2 và cạnh bên bằng \(2\sqrt3\) . Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC
-
Hình nón có thiết diện cắt bởi mặt phẳng qua trục là một tam giác vuông và có diện tích xung quanh là \(\sqrt 2 \). Độ dài đường cao của hình nón là:
-
Diện tích toàn phần của hình nón có khoảng cách từ tâm của đáy đến đường sinh bằng \(\sqrt3\)và thiết diện qua trục là tam giác đều là
-
Diện tích xung quanh của mặt trụ có bán kính đáy R, chiều cao h là
-
Một hình trụ có bán kính 5cm và chiều cao 7cm. Cắt khối trụ bằng một mặt phẳng song song với trục và cách trục 3cm. Diện tích thiết diện tạo bởi khối trụ và mặt phẳng bằng
-
Người ta xếp hai quả cầu có cùng bán kính (r ) vào một chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ (tham khảo hình vẽ). Biết thể tích khối trụ là 120cm3, thể tích của mỗi khối cầu bằng
-
Hình nón tròn xoay ngoại tiếp tứ diện đều SABC cạnh a, có diện tích xung quanh là:
-
Một khối trụ có bán kính đáy bằng (2 ), chiều cao bằng (3 ). Tính thể tích (V ) của khối trụ.
-
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua trục là một hình vuông. Thể tích khối trụ là:
-
Cho hình chữ nhật ABCD có AB = 2AD. Lần lượt quay hình chữ nhật quanh các trục AB, AD ta được hai khối trụ lần lượt gọi là (H1), (H2). Tính tỉ số thể tích của khối trụ (H1) chia cho thể tích của khối trụ (H2)
-
Hình nón có đường cao 20cm, bán kính đáy 25cm. Một mặt phẳng (P) qua đỉnh của hình nón và có khoảng cách đến tâm là 12cm. Diện tích thiết diện tạo bởi (P) và hình nón là:
