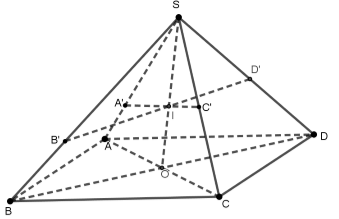
Cho hình chóp (S.ABCD ) có đáy (ABCD ) là hình bình hành. Gọi (A' ) là điểm trên (SA ) sao cho ( \( \overrightarrow {AA'} = \frac{1}{2}\overrightarrow {A'S} \) ). Mặt phẳng ( \( \alpha \) ) qua (A' ) cắt các cạnh (SB ), (SC ), (SD ) lần lượt tại (B' ), (C' ), (D' ). Tính giá trị của biểu thức \( T = \frac{{SB}}{{SB'}} + \frac{{SD}}{{SD'}} - \frac{{SC}}{{SC'}}\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi O là giao của AC và BD. Ta có O là trung điểm của đoạn thẳng AC, BD.
Các đoạn thẳng SO,A′C′, B′D′ đồng quy tại I
Ta có:
\(\begin{array}{l} {S_{SA'I}} + {S_{SC'I}} = {S_{SA'C'}} \Leftrightarrow \frac{{{S_{SA'I}}}}{{{S_{SAC}}}} + \frac{{{S_{SC'I}}}}{{{S_{SAC}}}} = \frac{{{S_{SA'C'}}}}{{{S_{SAC}}}}\\ \Leftrightarrow \frac{{{S_{SA'I}}}}{{2{S_{SAO}}}} + \frac{{{S_{SC'I}}}}{{2{S_{SCO}}}} = \frac{{{S_{SA'C'}}}}{{{S_{SAC}}}} \Leftrightarrow \frac{{SA'}}{{2SA}}.\frac{{SI}}{{SO}} + \frac{{SC'}}{{2SC}}.\frac{{SI}}{{SO}} = \frac{{SA'}}{{SA}}.\frac{{SC'}}{{SC}}\\ \Leftrightarrow \frac{{SI}}{{2SO}}\left( {\frac{{SA'}}{{SA}} + \frac{{SC'}}{{SC}}} \right) = \frac{{SA'}}{{SA}}.\frac{{SC'}}{{SC}} \Leftrightarrow \frac{{SA}}{{SA'}} + \frac{{SC}}{{SC'}} = 2.\frac{{SO}}{{SI}} \end{array}\)
Tương tự:
\(\begin{array}{l} \frac{{SB}}{{SB'}} + \frac{{SD}}{{SD'}} = 2.\frac{{SO}}{{SI}}\\ \to \frac{{SB}}{{SB'}} + \frac{{SD}}{{SD'}} - \frac{{SC}}{{SC'}} = \frac{{SA}}{{SA'}} = \frac{3}{2} \end{array}\)