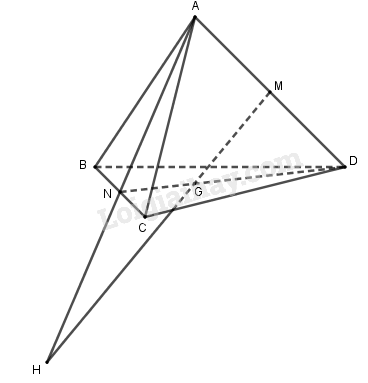
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC, G là trọng tâm tam giác BCD. Khi ấy giao tuyến của MG và mặt phẳng (ABC) là
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTa có: AN=(ADN)∩(ABC)
Trong (ADN), MG và AN không song song (vì \( \frac{{DM}}{{DA}} = \frac{1}{2} \ne \frac{2}{3} = \frac{{DG}}{{DN}}\)) nên gọi H=AN∩MG
Khi đó
\(\left\{ \begin{array}{l} H \in AC \subset (ABC)\\ H \in MG \end{array} \right. \to H = MG \cap (ABC)\)
Vậy giao điểm của MG và mặt phẳng (ABC) là giao điểm của MG với AN.
Chọn đáp án: D
ADMICRO
YOMEDIA
ZUNIA9