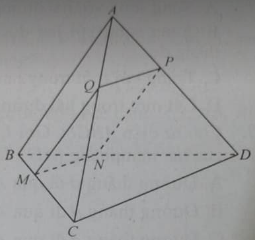
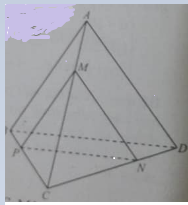
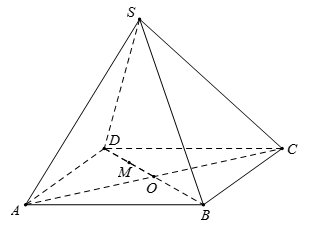
Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình bình hành tâm​​ O. Lấy điểm​​ I​​ trên đoạn​​ SO​​ sao cho​​ \(\dfrac{SI}{SO}=\dfrac23\),​​ BI​​ cắt​​ SD​​ tại​​ M​​ và​​ DI​​ cắt​​ SB​​ tại​​ N.​​ MNBD​​ là hình gì ?

Câu hỏi liên quan

• Cho tứ diện ABCD. Giả sử M thuộc đoạn BC. Một mặt (∝) qua M song song với AB và CD. Thiết diện của (∝) và hình tứ diện ABCD là hình gì?

  

• Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?

• Cho tứ diện ABCD, điểm M thuộc AC. Mặt phẳng (∝) đi qua M, song song với AB và AD. Thiết diện (∝) với tứ diện ABCD là hình gì?

  

ZUNIA12

• Trong các mệnh đề sau mệnh đề nào đúng?

• Cho tứ diện ABCD, các điểm E, F, G, H lần lượt thuộc các cạnh AD, AB, BC, CD sao cho

  \(\frac{{EA}}{{ED}} = \frac{{FA}}{{FB}} = \frac{{GC}}{{GB}} = \frac{{HC}}{{HD}}\)

  Khẳng định nào sau đây là đúng?

• Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng \((\alpha)\) qua BD và song song với SA, mặt phẳng \((\alpha)\) cắt SC tại K. Khẳng định nào sau đây là khẳng định đúng ?

• Cho tứ diện​​ ABCD​​ có​​ AB = CD. Mặt phẳng​​ α​​ qua trung điểm của​​ AC​​ và song song vớiAB,​​ CD​​ cắt​​ ABCD​​ theo thiết diện là

• Cho hai đường thẳng phân biệt a và b cùng song song với mp (P). Có bao nhiêu vị trí tương đối của a và b?

• Cho tứ diện​​ ABCD​​ với​​ M, N​​ lần lượt là trọng tâm các tam giác​​ ABD​​ ,​​ ACD

  Xét các khẳng định sau:

  (I)​​ MN ∥ mpABC.

  (II)​​ MN ∥ mpBCD.

  (III)​​ MN ∥ mpACD.

  (IV) MN ∥ mpCDA.

  Các mệnh đề nào đúng?

• Cho hình chóp​​ S.ABCD​​ có đáy​​ ABCD​​ là hình bình hành. Mặt phẳng​​ α​​ qua​​ BD​​ và song song với​​ SA, mặt phẳng​​ α​​ cắt​​ SCtại​​ K.​​ Khẳng định nào sau đây là khẳng định đúng ?​​ 

• Cho đường thẳng a và mặt phẳng (P) song song với nhau. Khi đó, số đường thẳng phân biệt nằm trong (P) và song song với a là

• Trong các mệnh đề sau, mệnh đề nào đúng?

• Cho hình chóp S.ABCD có đáy là hình vuông. Gọi (O ) là giao điểm của (AC ) và (BD ), (M ) là trung điểm của (DO ), ( \(\alpha\) ) là mặt phẳng đi qua (M ) và song song với AC và SD. Thiết diện của hình chóp cắt bởi mặt phẳng (\(\alpha\)) là hình gì.

  

• Cho hình chóp S.ABCD. Gọi A’, B’, C’, D’ lần lượt là trung điểm  của các cạnh SA, SB, SC, SD. Một mặt phẳng (P) thay đổi qua A’ và song song với AC luôn đi qua một đường thẳng cố định là:

• Cho một mặt phẳng (P) và hai đường thẳng song song a, b. Mệnh đề nào sau đây là sai?

• Cho hình chóp (S.ABCD )có đáy ABCD là hình thang (AB//CD). Gọi I,J lần lượt là trung điểm của các cạnh AD, BC và G là trọng tâm tam giác (SAB ). Biết thiết diện của hình chóp cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sao đây đúng?

• Cho hình hộp (ABCD.A'B'C'D' ). Gọi (M ) là điểm trên cạnh (AC ) sao cho (AC = 3MC ). Lấy (N ) trên cạnh (C'D ) sao cho (C'N = xC'D ). Với giá trị nào của (x ) thì (MN //BD' ).

• Những quy tắc nào sau đây không đúng với quy tắc vẽ hình trong không gian:

• Cho tứ diện ABCD và M là điểm ở trên cạnh AC. Mặt phẳng \((\alpha)\) qua và M song song với AB và CD. Thiết diện của tứ diện cắt bởi \((\alpha)\) là

• Cho hai đường thẳng a và b chéo nhau.

  Có bao nhiêu mặt phẳng chứa​​ a​​ và song song với b?