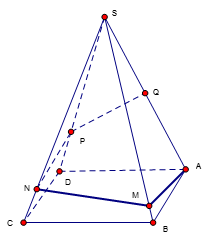
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có \( AB = a\sqrt 2 \). Cạnh bên SA = 2a và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ D đến mặt phẳng (SBC)

Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc với nhau, OA = OB = OC = a. Gọi I là trung điểm BC. Khoảng cách giữa AI và OC bằng bao nhiêu?

Cho hình chóp S.ABCD có \(SA \bot \left( {{\rm{ }}ABCD} \right)\), đáy ABCD là hình thang vuông có chiều cao AB = a. Gọi I và J lần lượt là trung điểm của AB và CB. Tính khỏang cách giữa đường thẳng IJ và (SAD).

Cho hình chóp S.ABCD có SD vuông góc với \(\left( {ABCD} \right), SD = {\rm{a}}\sqrt 5 \). Đáy ABCD là hình thang vuông tại A và D với CD = 2AD = 2AB = 2a. Gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thằng AC và SM.

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Gọi M là trung điểm của CD. Khoảng cách từ M đến (SAB) nhận giá trị nào trong các giá trị sau?

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B biết \(BC=a\sqrt{3}\), \(BA=a\). Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AC và biết thể tích khối chóp S.ABC bằng\(\frac{{{a}^{3}}\sqrt{6}}{6}\). Khoảng cách h từ C đến mặt phẳng (SAB) là.

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a và cạnh bên bằng \(\frac{{a\sqrt {37} }}{3}\). Gọi M là trung điểm cạnh SA. Tính khoảng cách giữa hai đường thẳng AC và BM.

Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC, A'D'. Tính khoảng cách giữa hai mặt phẳng \(\left( {MNP} \right){\rm{ và }}\left( {{\rm{ }}ACC'} \right).\)

Cho hình chóp O.ABC có đường cao \(OH = \frac{{2a}}{{\sqrt 3 }}\). Gọi M và N lần lượt là trung điểm của OA và OB. Khoảng cách giữa đường thẳng MN và (ABC) bằng

Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AC = a, I là trung điểm SC. Hình chiếu vuông góc của S lên \(\left( {ABC} \right)\) là trung điểm H của BC. Mặt phẳng \(\left( {SAB} \right)\) tạo với \(\left( {ABC} \right)\) một góc \(60^\circ \). Tính khoảng cách từ I đến mặt phẳng \(\left( {SAB} \right)\).

Cho hình thang vuông ABCD vuông ở A, D, AD = 2a. Trên đường thẳng vuông góc với (ABCD) tại D lấy điểm S với \(SD = a\sqrt 2 .\) Tính khoảng cách giữa DC và (SAB).

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa BB' và AC bằng:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right)\), SA = a. Gọi G là trọng tâm tam giác ABD, khi đó khoảng cách từ điểm G đến mặt phẳng \(\left( {SBC} \right)\) bằng

Cho hình lập phương (ABCD.A'B'C'D' ) có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD' bằng

Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều cạnh AB = 2a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của AB. Biết góc giữa cạnh bên và mặt đáy bằng 60⁰ . Tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC'A')

Cho hình chóp S.ABCD có \(SA \bot \left( {{\rm{ }}ABCD} \right),\) mặt đáy ABCD là hình thang vuông có chiều cao AB = a. Gọi I và J lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa đường thẳng IJ và (SAD).

Trong mặt phẳng (P) cho tam giác đều ABC cạnh a. Trên tia Ax vuông góc với mặt phẳng (P) lấy điểm S sao cho SA = a. Khoảng cách từ A đến (SBC) bằng bao nhiêu?

Cho hình chóp S.ABCD có \(V = {a^3}\sqrt 3 \). Đáy là hình vuông cạnh a, hãy tính khoảng cách từ S đến mặt phẳng ABCD.

Cho lăng trụ tam giác \(ABC.{{A}_{1}}{{B}_{1}}{{C}_{1}}\) có tất cả các cạnh bằng a, góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30⁰. Hình chiếu H của điểm A lên mặt phẳng \(\left( {{A}_{1}}{{B}_{1}}{{C}_{1}} \right)\) thuộc đường thẳng B₁C₁. Khoảng cách giữa hai đường thẳng AA₁ và BC₁ theo a là:  

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(AB=1,AC=\sqrt{3}\). Tam giác SBC đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách từ B đến mặt phẳng (SAC).

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 4, AD = 3. Mặt phẳng (ACD') tạo với mặt đáy một góc 60^O. Tính khoảng cách giữa hai mặt đáy của hình hộp.