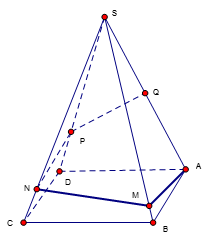
Bên cạnh con đường trước khi vào thành phố người ta xây một ngọn tháp đèn lộng lẫy. Ngọn tháp hình tứ giác đều S.ABCD cạnh bên SA = 600 mét, góc \( \widehat {SAB} = {15^0}\) . Do có sự cố đường dây điện tại điểm Q (là trung điểm của SA) bị hỏng, người ta tạo ra một con đường từ A đến Q gồm bốn đoạn thẳng: AM, MN, NP, PQ (hình vẽ). Để tiết kiệm kinh phí, kỹ sư đã nghiên cứu và có được chiều dài con đường từ A đến Q ngắn nhất. Tính tỉ số \( k = \frac{{AM + MN}}{{NP + PQ}}\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGiả sử trải các mặt hình chóp đều trên đường tròn tâm S và bán kính R=SA. Ta cóΔSAK có \( \widehat {ASK} = {15^ \circ }.4 = {60^ \circ }\)⇒ΔSAK đều.
Mà đoạn đường AQ ngắn nhất khi A, M, N, P, Q thẳng hàng.
Khi đó N là trọng tâm ΔSAK. Suy ra
\( k = \frac{{AM + MN}}{{NP + PQ}} = \frac{{AN}}{{NQ}} = 2\)

.png)











