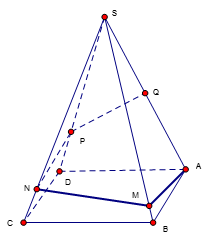
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt{3}\). SA vuông góc với đáy và SC = 3a. Khoảng cách từ điểm A đến mp(SCD) là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi H là hình chiếu của A lên SD.
\(SA\bot \left( ABCD \right)\Rightarrow SA\bot CD\), \(CD\bot AD\Rightarrow CD\bot \left( SAD \right)\Rightarrow \left( SAD \right)\bot \left( SCD \right)\) mà \(\left( SAD \right)\cap \left( SCD \right)=SD\)
Nên \(AH\bot \left( SCD \right)\), do đó \(d\left( A,\left( SCD \right) \right)=AH\).
Hình vuông ABCD cạnh \(a\sqrt{3}\) có đường chéo \(AC=a\sqrt{3}.\sqrt{2}=a\sqrt{6}\)
Tam giác SAC vuông tại A theo định lí Pytago ta tính được \(SA=a\sqrt{3}\)
Tam giác SAD vuông tại A có AH là đường cao nên \(\frac{1}{A{{H}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{D}^{2}}}\text{ hay }\frac{1}{A{{H}^{2}}}=\frac{1}{3{{a}^{2}}}+\frac{1}{3{{a}^{2}}}=\frac{2}{3{{a}^{2}}}\Leftrightarrow AH=\frac{a\sqrt{6}}{2}\)
Câu hỏi liên quan
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA=a\) và vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng AB và SC
-
Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a. Hình chiếu của S lên mặt phẳng đáy trùng với trung điểm H của AD và \(SH = \frac{{a\sqrt 6 }}{2}.\) Tính khoảng cách d từ B đến mặt phẳng \(\left( {SCD} \right)\).
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính theo a khoảng cách từ điểm A đến mặt phẳng (A'BC)
-
Cho hàm số S.ABC có \(ASB=BSC=CSA={{60}^{0}},SA=3,SB=4,SC=5\). Tính khoảng cách từ C đến mặt phẳng (SAB).
-
Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a2. Khoảng cách từ S đến BC bằng bao nhiêu?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AD, DC. Gọi H là giao điểm của CN và DM, biết SH vuông góc (ABCD), \(SH = a\sqrt 3 \). Khoảng cách từ điểm C đến mặt phẳng (SBP) tính theo a bằng
-
Cho hình chóp S.ABCD có \(V = {a^3}\sqrt 3 \). Đáy là hình vuông cạnh a, hãy tính khoảng cách từ S đến mặt phẳng ABCD.
-
Cho lăng trụ \(ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\) có đáy ABCD là hình chữ nhật. AB = a, AD = \(a\sqrt{3}\). Hình chiếu vuông góc của điểm A1 trên mặt phẳng (ABCD) trùng với giao điểm AC và \(BD.\) Góc giữa hai mặt phẳng (ADD1A1) và (ABCD) bằng 600. Tính khoảng cách từ điểm B1 đến mặt phẳng (A1BD) theo a.
-
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng \(a\sqrt 2 \). Tính khoảng cách d từ tâm O của đáy ABCD đến một mặt bên theo a.
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khi đó, khoảng cách giữa hai mặt phẳng (CB'D') và (BDA') bằng
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a. Cạnh bên \( SA = a\sqrt 2 \) và vuông góc với đáy (ABCD). Tính khoảng cách d từ điểm B đến mặt phẳng (SCD)
-
Cho hình chóp S.ABCD có \(SA \bot \left( {ABCD} \right)\), đáy ABCD là hình chữ nhật với \(AC = a\sqrt 5 \) và \(BC = a\sqrt 2 \). Tính khoảng cách giữa SD và BC.
-
Cho hình chóp (S.ABCD ) có đáy ABCD là hình vuông, \(\frac{{SB}}{{\sqrt 2 }} = \frac{{SC}}{{\sqrt 3 }} = a\). Cạnh SA vuông góc (ABCD), khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
-
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD với \(AB=2a,BC=a\). Các cạnh bên của hình chóp bằng nhau và bằng \(a\sqrt{2}\). Khoảng cách từ A đến mp (SCD) là:
-
Xét tứ diện (OABC ) có (OA ), (OB ), (OC ) đôi một vuông góc. Gọi \(\alpha, \beta, \gamma \) lần lượt là góc giữa các đường thẳng (OA ), (OB ), (OC ) với mặt phẳng (ABC) (hình vẽ).
Khi đó giá trị nhỏ nhất của biểu thức \( M = \left( {3 + {{\cot }^2}\alpha } \right).\left( {3 + {{\cot }^2}\beta } \right).\left( {3 + {{\cot }^2}\gamma } \right)\)
-
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khoảng cách giữa (ACB') và (DA'C') bằng
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a, \(SA = SB = SC = SD = a\sqrt 5 \). Tính khoảng cách từ điểm B đến mặt phẳng \(\left( {SCD} \right)\).
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa BB' và AC bằng
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông \(BD=2a,\Delta SAC\) vuông tại S và nằm trong mặt phẳng vuông góc với đáy, \(SC=a\sqrt{3}\). Khoảng cách từ điểm B đến mặt phẳng (SAD) là:
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh \(a\). Cạnh bên \(SA\) vuông góc với đáy, góc \(\widehat{SBD}={{60}^{0}}\). Tính theo \(a\) khoảng cách giữa hai đường thẳng \(AB\) và \(SO\).
