Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu của S lên mặt phẳng \(\left( {ABCD} \right)\) là điểm H sao cho \(2\overrightarrow {HA} + \overrightarrow {HB} = \overrightarrow 0 \). Góc giữa đường thẳng SB và đáy bằng \({45^0}\). Tính cos góc giữa đường thẳng SD và mặt phẳng \(\left( {SBC} \right)\).
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
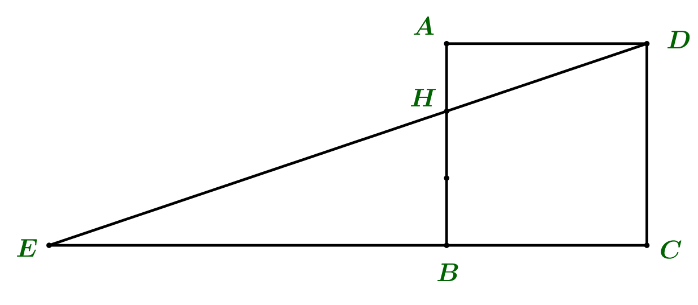
Không mất tính tổng quát, giả sử đáy ABCD là hình vuông cạnh bằng 3.
Từ giả thiết \(2\overrightarrow {HA} + \overrightarrow {HB} = \overrightarrow 0 \Rightarrow H\) là điểm thuộc đoạn AB và HB = 2HA
\( \Rightarrow HB = 2,\,HA = 1\).
Gọi \(\varphi \) là góc giữa đường thẳng SD và mặt phẳng \(\left( {SBC} \right)\), khi đó \(\sin \varphi = \frac{{d\left( {D,\left( {SBC} \right)} \right)}}{{SD}}\).
Gọi \(E = HD \cap BC\).
Ta có \(\frac{{DE}}{{HE}} = \frac{{CD}}{{HB}} = \frac{3}{2} \Rightarrow \frac{{d\left( {D,\left( {SBC} \right)} \right)}}{{d\left( {H,\left( {SBC} \right)} \right)}} = \frac{{DE}}{{HE}} = \frac{3}{2} \Rightarrow d\left( {D,\left( {SBC} \right)} \right) = \frac{3}{2}d\left( {H,\left( {SBC} \right)} \right)\)
Kẻ \(HK \bot SB,\,\,K \in SB\)
Ta có \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot HK\)
Có \(\left\{ \begin{array}{l}HK \bot SB\\HK \bot BC\end{array} \right. \Rightarrow HK \bot \left( {SBC} \right) \Rightarrow d\left( {H,\left( {SBC} \right)} \right) = HK\).
Góc giữa đường thẳng SB và \(\left( {ABCD} \right)\) là góc \(\widehat {SBH} = {45^0}\)
Trong tam giác vuông BHK có \(HK = BH.\sin 45^\circ = 2.\frac{{\sqrt 2 }}{2} = \sqrt 2 \).
Ta có \(SH = BH.\tan 45^\circ = 2\) và \(HD = \sqrt {A{D^2} + A{H^2}} = \sqrt {{3^2} + {1^2}} = \sqrt {10} \)
\( \Rightarrow SD = \sqrt {S{H^2} + H{D^2}} = \sqrt {14} \)
Do đó, \(\sin \varphi = \frac{{d\left( {D,\left( {SBC} \right)} \right)}}{{SD}} = \frac{3}{2}\frac{{HK}}{{SD}} = \frac{{3\sqrt 7 }}{{14}} \Rightarrow \cos \varphi = \frac{{\sqrt {133} }}{{14}}\).
Câu hỏi liên quan
-
Cho tứ diện đều S.ABC có tất cả các cạnh bằng nhau. Gọi \(M,\,N\) lần lượt là trung điểm của SA và BC. Tính cos góc giữa đường thẳng MN và mặt phẳng \(\left( {SBC} \right)\)
-
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB = SD. Đường thẳng DB không vuông góc với đường thẳng nào sau đây?
-
Cho hình chóp S.ABC có cạnh \(S A \perp(A B C)\) và đáy ABC là tam giác cân ở C . Gọi H và K lần lượt là trung điểm của AB và SB . Khẳng định nào sau đây sai?
-
Các đường thẳng cùng vuông góc với một đường thẳng thì:
-
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Gọi M là trung điểm của AD và K là trung điểm của BD
Góc giữa CM với mặt phẳng (BCD) là:
-
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng nhau. Tính cos góc giữa đường thẳng SA và mặt phẳng \(\left( {SCD} \right)\)
-
Đường thẳng a vuông góc với hai đường thẳng phân biệt trong mặt phẳng (P) thì:
-
Cho hình thoi ABCD có tâm O , \(A C=2 a ; B D=2 \mathrm{AC}\) . Lấy điểm S không thuộc (ABCD) sao cho \(S O \perp(A B C D)\). Biết \(\tan \widehat{S B O}=\frac{1}{2}\) . Tính số đo của góc giữa SC và (ABCD)?
-
Các đường thẳng cùng vuông góc với một đương thẳng thì:
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(\alpha \) là góc giữa đường thẳng SC và đáy. Khẳng định nào sau đây đúng?
-
Cho hình chóp S.ABC, có cạnh bên \(SA \bot \left( {ABC} \right)\). Góc giữa đường thẳng SB và đáy là góc nào dưới đây?
-
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc.
Khằng định nào sau đây đúng?
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh \(SA \bot \left( {ABC} \right)\) và SA = 2a, gọi M là trung điểm của SC. Tính cos của góc \(\alpha \) là góc giữa đường thẳng BM và \(\left( {ABC} \right)\).
-
Cho hình chóp \(S \cdot A B C \text { có } S A=S B=S C\) và tam giác ABC vuông tại B . Vẽ \(S H \perp(A B C), H \in(A B C)\). Khẳng định nào sau đây đúng?
-
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng BC vuông góc với đường thẳng
-
Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng a và \(S A \perp(A B C D)\). Biết \(S A=\frac{a \sqrt{6}}{3}\) . Tính góc giữa SC và (ABCD)?
-
Cho tứ diện ABCD có cạnh AB , BC , BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
-
Cho khối chóp S.ABC có SA vuông góc với mặt phẳng \(\left( {ABC} \right)\) và SA = a. Đáy ABC thỏa mãn \(AB = a\sqrt 3 \). Tìm số đo góc giữa đường thẳng SB và mặt phẳng \(\left( {ABC} \right)\)
-
Cho góc tam diện Sxyz với\(\widehat{x S y}=120^{\circ}, \widehat{y S z}=60^{\circ}, \widehat{z S x}=90^{\circ}\) . 0 Trên các tia \(S x, S y, S z\) lần lượt
lấy các điểm A, B, C sao cho \(S A=S B=S C=a\) . Tam giác ABC có đặc điểm nào trong các số các đặc
điểm sau : -
Các đường thẳng cùng vuông góc với một đường thẳng thì:
