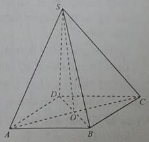
Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng a và \(S A \perp(A B C D)\). Biết \(S A=\frac{a \sqrt{6}}{3}\) . Tính góc giữa SC và (ABCD)?

Câu hỏi liên quan

•  Cho hình chóp S.ABCD có đáy ABCD là hình vuông, Gọi H là trung điểm của AB và \(S H \perp(A B C D)\). Gọi K là trung điểm của cạnh AD . Khẳng định nào sau đây là sai?

• Cho hình chóp S.ABCD  có đáy ABCD là hình thoi, O là giao điểm của 2 đường chéo và SA= SC . Các khẳng định sau, khẳng định nào đúng? 

• Cho hình lập phương ABCD.A’B’C’D’. Tính \({\mathop{\rm Cos}\nolimits} in\) giữa đường thẳng A’C và mặt phẳng \(\left( {ABB’A’} \right)\)

ZUNIA12

• Khẳng định nào sau đây đúng?

• Cho hình chóp S ABCD . có đáy ABCD là hình vuông cạnh a , \(S A \perp(A B C D), S A=a \sqrt{6}\) . Gọi \(\alpha\) là góc giữa SC và mp \((S A B)\). Chọn khẳng định đúng trong các khẳng định sau?

• Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc.

  Khằng định nào sau đây đúng?

• Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, biết \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt 5 \). Gọi M là trung điểm của SB. Tính góc giữa đường thẳng CM và \(\left( {ABCD} \right)\)

• Cho hình thoi ABCD có tâm O , \(A C=2 a ; B D=2 \mathrm{AC}\) . Lấy điểm S không thuộc (ABCD) sao cho \(S O \perp(A B C D)\). Biết \(\tan \widehat{S B O}=\frac{1}{2}\) . Tính số đo của góc giữa SC và (ABCD)?

• Cho hình lập phương ABCD.A’B’C’D’. Tính \(\cos in\) góc giữa đường thẳng AC và mặt phẳng \(\left( {A’CD} \right)\)

• Cho góc tam diện Sxyz với\(\widehat{x S y}=120^{\circ}, \widehat{y S z}=60^{\circ}, \widehat{z S x}=90^{\circ}\) . 0 Trên các tia \(S x, S y, S z\) lần lượt
  lấy các điểm A, B, C  sao cho \(S A=S B=S C=a\) . Tam giác ABC có đặc điểm nào trong các số các đặc
  điểm sau :

• Cho hình chóp S.ABCD, đáy là hình thoi tâm O và SA = SC, SB = SD

  Đường thẳng AC vuông góc với mặt phẳng

  

• Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ (ABCD) Tam giác SOD là:

  

• Cho lăng trụ đứng ABC.A’B’C’, có đáy là tam giác vuông cân tại B và \(AC = a\sqrt 2 \) ; cạnh bên AA’ = a. Gọi N là trung điểm của A’C’. Tính góc giữa đường thẳng AN và mặt phẳng \(\left( {A’BC} \right)\).

• Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh \(SA \bot \left( {ABC} \right)\) và SA = 2a, gọi M là trung điểm của SC. Tính cos của góc \(\alpha \) là góc giữa đường thẳng BM và \(\left( {ABC} \right)\).

• Cho hình chóp đều S.ABCD có tất cả các cạnh bằng nhau. Gọi M, N lần lượt là trung điểm của SA và CD. Tính cos góc giữa đường thẳng MN và mặt phẳng \(\left( {SCD} \right)\)

• Cho tứ diện ABCD có \(A B=A C \text { và } D B=D C\) . Khẳng định nào sau đây đúng? 

• Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt 6 \). Gọi M là trung điểm của SC. Tính góc giữa đường thẳng BM và \(\left( {ABCD} \right)\)

• Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu của S lên mặt phẳng \(\left( {ABCD} \right)\) là điểm H sao cho \(2\overrightarrow {HA} + \overrightarrow {HB} = \overrightarrow 0 \). Góc giữa đường thẳng SB và đáy bằng \({45^0}\). Tính cos góc giữa đường thẳng SD và mặt phẳng \(\left( {SBC} \right)\).

• Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng AC và C’D’ bằng:

  

• Tập hợp các điểm cách đều ba đỉnh của tam giác ABC là: