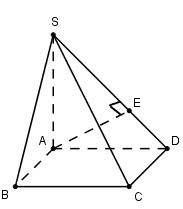
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a. Cạnh bên \( SA = a\sqrt 2 \) và vuông góc với đáy (ABCD). Tính khoảng cách d từ điểm B đến mặt phẳng (SCD)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Do AB // CD nên \( d\left( {B;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)\)
Kẻ AE⊥SD tại E. (1)
Ta có: \(\left\{ \begin{array}{l} CD \bot AD\\ CD \bot SA \end{array} \right. \Rightarrow CD \bot (SAD) \Rightarrow CD \bot AE(2)\)
Từ (1) và (2) ⇒ AE⊥(SCD)
Khi đó \( d\left( {A;\left( {SCD} \right)} \right) = AE.\)
Tam giác vuông SAD, có \( AE = \frac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{{a\sqrt 6 }}{3}.\)
Vậy \( d\left( {B;\left( {SCD} \right)} \right) = AE = \frac{{a\sqrt 6 }}{3}.\)
Câu hỏi liên quan
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng cách từ A đến mặt phẳng \(\left( {SBD} \right)\) bằng
.png)
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABD. Cạnh bên SD tạo với mặt phẳng (ABCD) một góc bằng 60o. Khoảng cách từ A tới mặt phẳng (SBC) tính theo a bằng
-
Cho hình thang vuông ABCD vuông ở A, D, AD = 2a. Trên đường thẳng vuông góc với (ABCD) tại D lấy điểm S với \(SD = a\sqrt 2 .\) Tính khoảng cách giữa DC và (SAB).
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Khoảng cách từ M đến SA nhận giá trị nào trong các giá trị sau?
-
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AC = a, I là trung điểm SC. Hình chiếu vuông góc của S lên \(\left( {ABC} \right)\) là trung điểm H của BC. Mặt phẳng \(\left( {SAB} \right)\) tạo với \(\left( {ABC} \right)\) một góc \(60^\circ \). Tính khoảng cách từ I đến mặt phẳng \(\left( {SAB} \right)\).
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B biết \(BC=a\sqrt{3}\), \(BA=a\). Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AC và biết thể tích khối chóp S.ABC bằng\(\frac{{{a}^{3}}\sqrt{6}}{6}\). Khoảng cách h từ C đến mặt phẳng (SAB) là.
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính theo a khoảng cách từ điểm A đến mặt phẳng (A'BC)
-
Cho hình chóp S.ABCD có SD vuông góc với \(\left( {ABCD} \right), SD = {\rm{a}}\sqrt 5 \). Đáy ABCD là hình thang vuông tại A và D với CD = 2AD = 2AB = 2a. Gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thằng AC và SM.
-
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khoảng cách giữa (ACB') và (DA'C') bằng
-
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AD = a, AB = 2a, BC = 3a, SA = 2a, H là trung điểm cạnh AB, SH là đường cao của hình chóp S.ABCD Tính khoảng cách từ điểm A đến mặt phẳng (SCD).
-
Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều cạnh AB = 2a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của AB. Biết góc giữa cạnh bên và mặt đáy bằng 600 . Tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC'A')
-
Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng alpha . Khoảng cách từ tâm của đáy đến một cạnh bên bằng
-
Cho hình lăng trụ tam giác \(ABC.{A_1}{B_1}{C_1}\) có cạnh bên bằng a. Các cạnh bên của lăng trụ tạo với mặt đáy góc 60o. Hình chiếu vuông góc của A lên mặt phẳng \(\left( {{A_1}{B_1}{C_1}} \right)\) là trung điểm của \({B_1}{C_1}.\) Khoảng cách giữa hai mặt đáy của lăng trụ bằng bao nhiêu?
-
Cho lăng trụ \(ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\) có đáy ABCD là hình chữ nhật. AB = a, AD = \(a\sqrt{3}\). Hình chiếu vuông góc của điểm A1 trên mặt phẳng (ABCD) trùng với giao điểm AC và \(BD.\) Góc giữa hai mặt phẳng (ADD1A1) và (ABCD) bằng 600. Tính khoảng cách từ điểm B1 đến mặt phẳng (A1BD) theo a.
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm 0, SA vuông góc với đáy (ABCD). Gọi K, H theo thứ tự là hình chiếu vuông góc của A và O lên SD. Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 4, AD = 3. Mặt phẳng (ACD') tạo với mặt đáy một góc 60O. Tính khoảng cách giữa hai mặt đáy của hình hộp.
-
Cho lăng trụ \(ABCD.A'B'C'D'\) có đáy ABCD là hình chữ nhật. \(AB=a,AD=a\sqrt{3}\). Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABCD) trùng với giao điểm AC và \(BD.\) Tính khoảng cách từ điểm B' đến mặt phẳng (A'BD) theo a là:
-
Cho hình chóp SABC, \(\Delta SAB\) đều cạnh a nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ C đến mặt phẳng \(\left( {SAB} \right)\) biết \(V = \frac{{{a^3}\sqrt 3 }}{6}\).
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông \(BD=2a,\Delta SAC\) vuông tại S và nằm trong mặt phẳng vuông góc với đáy, \(SC=a\sqrt{3}\). Khoảng cách từ điểm B đến mặt phẳng (SAD) là:
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1 (đvdt). Khoảng cách giữa AA' và BD' bằng:
