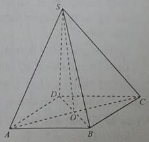
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, biết \(SA \bot \left( {ABCD} \right)\) và SA = 2a. Gọi M và N lần lượt là là trung điểm của \(BC,\,SD\). Tính góc giữa đường thẳng MN và \(\left( {ABCD} \right)\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi P là trung điểm của đoạn AD.
NP là đường trung bình của tam giác SAD nên \(NP = \frac{1}{2}SA = a\) đồng thời \(NP \bot \left( {ABCD} \right)\).
Hình chiếu vuông góc của MN lên đáy \(\left( {ABCD} \right)\) là MP, cho nên
\(\left( {MN,\left( {ABCD} \right)} \right) = \left( {MN,MP} \right) = \widehat {PMN}\).
Trong tam giác vuông MNP ta có: \(\tan \widehat {PMN} = \frac{{NP}}{{MP}} = \frac{{NP}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {PMN} = 45^\circ \).
Vậy góc giữa MN và đáy bằng \(45^\circ \).
.png)