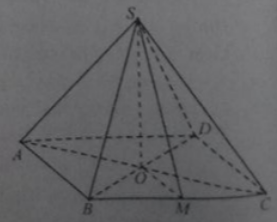
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi cạnh bên và mặt đáy.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
+ Vì \(SH \bot \left( {ABC} \right)\) và \(AN \subset \left( {ABC} \right) \Rightarrow SH \bot AN\) hay \(\Rightarrow SH \bot AH\) ⇒ AH là hình chiếu vuông góc của SA lên (ABC) ⇒ \(\left( {SA,\left( {ABC} \right)} \right) = \left( {SA,AH} \right) = \widehat {SAH}\)
+ Gọi M, N lần lượt là trung điểm của AC, BC.
Vì \(\Delta ABC\) là tam giác đều cạnh a nên dễ tính được : \(AN = \frac{{a\sqrt 3 }}{2}\).
Từ giả thiết suy ra H là trọng tậm \(\Delta ABC\).
\(\Rightarrow AH = \frac{2}{3}AN = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
+ Áp dụng hệ thức lượng trong tam giác SHA vuông tại H ta có:
\(\tan \widehat {SAH} = \frac{{SH}}{{AH}} = \frac{a}{{\frac{{a\sqrt 3 }}{3}}} = \sqrt 3 \Rightarrow \widehat {SAH} = 60^\circ \).
Câu hỏi liên quan
-
Cho hình chóp tứ giác đều có cạnh đáy bằng \(a\sqrt 2 \) và chiều cao bằng \(\frac{{a\sqrt 2 }}{2}\). Tính số đo của góc giữa mặt bên và mặt đáy.
-
Cho hình lập phương ABCD.A'B'C'D'. Xét mặt phẳng (A'BD). Trong các mệnh đề sau mệnh đề nào đúng?
-
Cho hình chóp S.ABC có SA = SB = SC = AB = AC = 1, \(B C=\sqrt{2}\). Tính góc giữa hai đường thẳng AB, SC
-
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và S, SA vuông góc với mặt phẳng đáy. Tính cô-sin góc giữa 2 đường thẳng SD và BC biết \(AD=D C=a, A B=2 a, S A=\frac{2 \sqrt{3} a}{3}\)
-
Cho hình chóp S.ABCD với ABCD là hình chữ nhật tâm O có \(AB = a,{\rm{ }}AD = 2a.{\rm{ }}SA\) vuông góc với đáy và SA = a. Gọi (P) là mặt phẳng qua SO và vuông góc với (SAD). Diện tích thiết diện của (P) và hình chóp S.ABCD bằng bao nhiêu?
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khẳng định nào sau đây sai?
-
Cho hình chóp cụt đều ABC.A'B'C' với đáy lớn ABC có cạnh bằng a. Đáy nhỏ A'B'C' có cạnh bằng \(\frac{a}{2}\), chiều cao \(OO' = \frac{a}{2}\). Khẳng định nào sau đây sai?
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \(B,\,\,SA \bot \left( {ABC} \right)\). Gọi E, F lần lượt là trung điểm của các cạnh AB và AC. Góc giữa hai mặt phẳng (SEF) và (SBC) là :
-
Cho tứ diện đều ABCD. Góc giữa (ABC) và (ABD) bằng \(\alpha\). Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tâm của đáy là O. Gọi M và N lần lượt là trung điểm của SA và BC. Biết rằng góc giữa MN và (ABCD) bằng 60o, cosin góc giữa MN và mặt phẳng (SBD) bằng :
-
Cho hai đường thẳng chéo nhau a và b đồng thời \(a \bot b\). Chỉ ra mệnh đề đúng trong các mệnh đề sau:
-
Cho hình chóp tam giác đều S.ABC với SA= 2AB . Góc giữa (SAB) và (ABC) bằng \(\alpha\) . Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình chóp S.ABC có \(S A \perp(A B C)\) và AB BC , gọi I là trung điểm BC . Góc giữa hai mặt phẳng \((S B C) \text { và }(A B C)\) là góc nào sau đây?
-
Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a. Độ dài cạnh bên của hình chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng 600 ?
-
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) . Góc giữa \(A^{\prime} C^{\prime} \text { và } D^{\prime} C^{\prime}\) là
-
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
Tan của góc giữa mặt bên và mặt đáy bằng:
-
Cho hình lăng trụ đứng tam giác ABC:A0B0C0 có đáy ABC là tam giác cân, \(A B=A C=a, \widehat{B A C}=120^{\circ}\)cạnh bên \(A A^{\prime}=a \sqrt{2}\). Tính góc giữa hai đường thẳng AB' và BC.
-
Cho hình lập phương \(A B C D . A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) cạnh a.Gọi M, N, P lần lượt là trung điểm các cạnh A B, B C, C'D'. Xác định góc giữa hai đường thẳng MN và AP.
-
Hình hộp ABCD.A'B'C'D' trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau đây?
-
Trong các mệnh đề sau, mệnh đề nào đúng?
