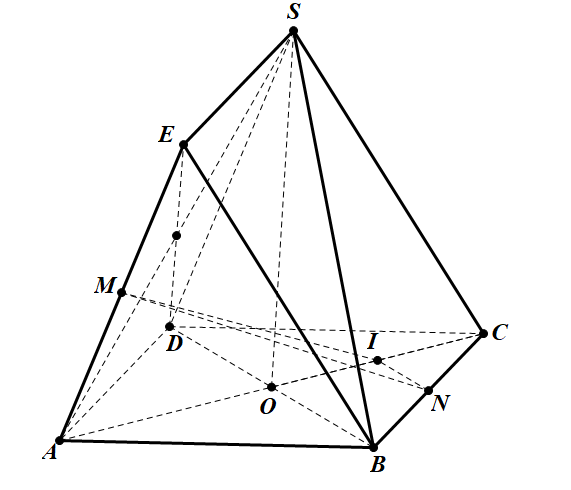
Cho hình chóp tứ giác đều S.ABCD đáy ABCD là hình vuông, E là điểm đối xứng với D qua trung điểm SA. Gọi M, N lần lượt là trung điểm của AE và BC. Góc giữa hai đường thẳng MN và BD bằng:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDo D đối xứng với E qua trung điểm của SA nên SDAE là hình bình hành, suy ra EA// SD. Ta có
\(\overrightarrow{M N}=\frac{\overrightarrow{A B}+\overrightarrow{E C}}{2}=\frac{\overrightarrow{A B}+\overrightarrow{E D}+\overrightarrow{D C}}{2}\)
\(\begin{array}{l} =\frac{\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{S D}+\overrightarrow{D C}}{2} \\ =\frac{\overrightarrow{A C}+\overrightarrow{S C}}{2} \end{array}\)
\(\text { Mà } B D \perp A C \text { và } B D \perp S C(\mathrm{~do}\, B \mathrm{D} \bot(S A C)) \text { nên }\)
\(\overrightarrow{B D} \cdot \overrightarrow{M N}=\overrightarrow{B D} \cdot \frac{\overrightarrow{A C}+\overrightarrow{S C}}{2}=0\)
\(\text { Vậy }(M N, B D)=90^{\circ} .\)