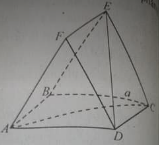
Cho tam giác đều ABC có cạnh bằng a và nằm trong mặt phẳng (P). Trên các đường thẳng vuông góc với (P) tại B, C lần lượt lấy D, E nằm trên cùng một phía đối với (P) sao cho \(BD = a\frac{{\sqrt 3 }}{2},CE = a\sqrt 3 \). Góc giữa (P) và (ADE) bằng bao nhiêu?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi \(\varphi = \left( {\left( {ABC} \right),\left( {ADE} \right)} \right)\).
Ta có: \({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\).
Mặt khác, ta có:
\(AD = \sqrt {A{B^2} + B{D^2}} = \sqrt {{a^2} + \frac{{3{a^2}}}{4}} = \frac{{a\sqrt 7 }}{2}\)
\(AE = \sqrt {A{C^2} + C{E^2}} = \sqrt {{a^2} + 3{a^2}} = 2a\)
Gọi F là trung điểm EC, ta có DF = BC = a.
Do đó \(DE = \sqrt {D{F^2} + F{E^2}} = \sqrt {{a^2} + \frac{{3{a^2}}}{4}} = \frac{{a\sqrt 7 }}{2}\).
Suy ra tam giác ADE cân tại D.
Gọi H là trung điểm AE, ta có \(DH = \sqrt {A{D^2} - A{H^2}} = \sqrt {\frac{{7{a^2}}}{4} - {a^2}} = \frac{{a\sqrt 3 }}{2}\).
Suy ra \({S_{ADE}} = \frac{1}{2}DH.AE = \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.2a = \frac{{{a^2}\sqrt 3 }}{2}\)
Vậy \(\cos \varphi = \frac{{{S_{ABC}}}}{{{S_{ADE}}}} = \frac{{\frac{{{a^2}\sqrt 3 }}{4}}}{{\frac{{{a^2}\sqrt 3 }}{2}}} = \frac{1}{2} \Rightarrow \varphi = {60^o}\).
Câu hỏi liên quan
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết \(SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \) và đường tròn nội tiếp ABCD có bán kính bằng a. Tính góc hợp bởi mỗi mặt bên với đáy.
-
Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC), tam giác ABC vuông cân ở A và có đường cao \(AH,{\rm{ }}(H \in BC)\). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?
-
Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai?
-
Cho hình chóp S.ABCD có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH \(\left( {H \in BC} \right)\). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây sai ?
-
Cho tam giác ABC vuông tại A. Cạnh AB = a nằm trong mặt phẳng (P), cạnh \(AC = a\sqrt 2 \), AC tạo với (P) một góc 60o. Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. \(SA \bot \left( {ABCD} \right)\), SA = x. Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60o.
-
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và S, SA vuông góc với mặt phẳng đáy. Tính cô-sin góc giữa 2 đường thẳng SD và BC biết \(AD=D C=a, A B=2 a, S A=\frac{2 \sqrt{3} a}{3}\)
-
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng A và góc \(\hat{A}=60^{\circ}\) , cạnh \(S C=\frac{a \sqrt{6}}{2}\) và SC vuông góc với mặt phẳng \((A B C D)\) . Trong tam giác SAC kẻ \(I K \perp S A\) tại K . Tính số đo góc \(\widehat{\mathrm{BKD}}\)
-
Cho tứ diện đều ABCD. Góc giữa (ABC) và (ABD) bằng \(\alpha\). Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(2a\sqrt 3 \) và cạnh bên bằng 2a. Gọi G và G' lần lượt là trọng tâm của hai đáy ABC và A'B'C'. Khẳng định nào sau đây đúng khi nói về AA'G'G?
-
Cho các mệnh đề sau với \((\alpha) \text { và }(\beta)\) là hai mặt phẳng vuông góc với nhau với giao tuyến \(m=(\alpha) \cap(\beta) \) và a, b, c, d là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?
-
Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng a. Tính số đo góc giữa (BA’C) và (DA’C)
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Tính AB theo a và x?
-
Tính cosin của góc giữa hai mặt của một tứ diện đều.
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Gọi M là trung điểm của SB. Góc giữa AM và BD bằng
-
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AD. Góc giữa hai đường thfẳng AB và CE bằng:
-
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60o. Gọi M và N lần lượt là trung điểm của AB và CD.
Đường vuông góc chung của AB và CD là:
-
Hình hộp ABCD.A'B'C'D' là hình hộp gì nếu tứ diện AA'B'D' có các cạnh đối vuông góc.
-
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau và OA=OB=OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
-
Cho hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\). Mặt phẳng \(\left( {{A_1}BD} \right)\) không vuông góc với mặt phẳng nào dưới đây?
