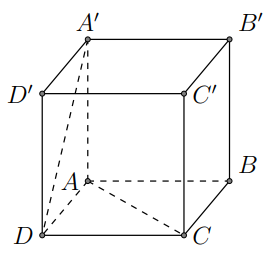
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\). Góc giữa hai đường thẳng AC và A'D bằng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(\begin{aligned} &\text { Ta có: } A C \| A^{\prime} C^{\prime} \Rightarrow\left(A C, A^{\prime} D\right)=\left(A^{\prime} C^{\prime}, A^{\prime} D\right) \text { . }\\ &\text { Mặt khác: } A^{\prime} C^{\prime}=A^{\prime} D=D C^{\prime}=a \sqrt{2} \text { nên suy ra } \triangle A^{\prime} D C^{\prime} \text { đều. }\\ &\text { Do đó }\left(A^{\prime} C^{\prime}, A^{\prime} D\right)=60^{\circ} \text { . } \end{aligned}\)
ADMICRO
YOMEDIA
ZUNIA9