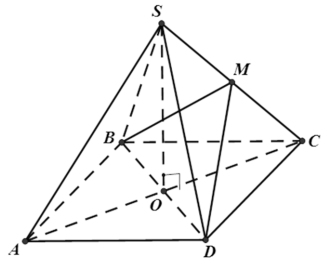
Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O . Các cạnh bên và các cạnh đáy đều bằng a . Gọi M là trung điểm SC . Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Gọi M' là trung điểm OC. Ta có
\(\begin{array}{l} S_{\triangle M B D}=\frac{1}{2} M O \cdot B D=\frac{1}{2} \cdot \frac{a}{2} \cdot a \sqrt{2}=\frac{a^{2} \sqrt{2}}{4} \\ S_{\triangle B M D}=\frac{1}{2} M^{\prime} O \cdot B D=\frac{1}{2} \cdot \frac{1}{4} \cdot a \sqrt{2} \cdot a \sqrt{2}=\frac{a^{2}}{4} \end{array}\)
Do đó \(\cos \alpha=\frac{S_{\triangle B M D}}{S_{\Delta B M D}}=\frac{\sqrt{2}}{2} \Rightarrow \alpha=45^{0}\)
Câu hỏi liên quan
-
Cho hình lập phương ABCD.A'B'C'D'. Xét mặt phẳng (A'BD). Trong các mệnh đề sau mệnh đề nào đúng?
-
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
-
Cho hình chóp S ABC . có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC) , tam giác ABC vuông cân ở A và có đường cao \(A H(H \in B C)\) . Gọi O là hình chiếu vuông góc của A lên (S B C) . Khẳng định nào sau đây sai ?
-
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân ở A. H là trung điểm BC. Khẳng định nào sau đây sai ?
-
Mệnh đề nào sau đây là đúng?
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tâm của đáy là O. Gọi M và N lần lượt là trung điểm của SA và BC. Biết rằng góc giữa MN và (ABCD) bằng 60o, cosin góc giữa MN và mặt phẳng (SBD) bằng :
-
Cho hình chóp cụt đều ABC.A'B'C' với đáy lớn ABC có cạnh bằng a. Đáy nhỏ A'B'C' có cạnh bằng \(\frac{a}{2}\), chiều cao \(OO' = \frac{a}{2}\). Khẳng định nào sau đây sai?
-
Cho hình chóp S,ABC có \(SA \bot \left( {ABC} \right)\) và \(AB \bot BC\), gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, \(SH=HC,SA=AB\). Gọi \(\alpha \) là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị của \(\tan \alpha \) là:
-
Cho hình chóp cụt tứ giác đều ABCD.A'B'C'D' cạnh của đáy nhỏ ABCD bằng \(\frac{a}{3}\) và cạnh của đáy lớn A'B'C'D' bằng a. Góc giữa cạnh bên và mặt đáy bằng 60o. Tính chiều cao OO' của hình chóp cụt đã cho.
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(S A \perp(A B C D)\), gọi O là tâm hình vuông ABCD . Khẳng định nào sau đây sai?
-
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAC) và (AHK) vuông góc vì:
.png)
-
Tứ diện đều ABCD cạnh a, M là trung điểm của cạnh CD. Cô-sin của góc giữa AM và BD là
-
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Người ta lấy trên giao tuyến d của hai mặt phẳng đó hai điểm A và B sao cho AB = 8. Gọi C là một điểm trên (P), D là một điểm trên (Q) sao cho AC, BD cùng vuông góc với giao tuyến d và AC = 6, BD = 24. Độ dài CD là:
-
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính của góc giữa một mặt bên và một mặt đáy.
-
Cho các mệnh đề sau với \((\alpha) \text { và }(\beta)\) là hai mặt phẳng vuông góc với nhau với giao tuyến \(m=(\alpha) \cap(\beta) \) và a, b, c, d là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?
-
Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc. Đường thẳng DE vuông góc?
-
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60o60o. Gọi M và N lần lượt là trung điểm của AB và CD.
Mặt phẳng (BCD) vuông góc với mặt phẳng
-
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AC = 2a. Các cạnh bên vuông góc với đáy và AA' = a. Khẳng định nào sau đây sai ?
