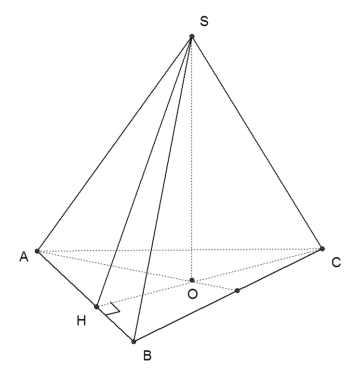
Cho hình chóp tam giác đều S.ABC với SA= 2AB . Góc giữa (SAB) và (ABC) bằng \(\alpha\) . Chọn khẳng định đúng trong các khẳng định sau?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi O là tâm của tam giác đều ABC
Gọi \(\mathrm{CO} \cap A B=H\) suy ra H là trung điểm AB( vì tam giác ABC đều).
\(\begin{aligned} &\Rightarrow O H \perp A B \text { và } O H=\frac{1}{3} C H=\frac{1}{3} \cdot \frac{A B \sqrt{3}}{2}=\frac{A B \sqrt{3}}{6}\\ &\text { Tìm góc giũa }(S A B) \text { và }(A B C)\\ &\left\{\begin{array}{c} (S A B) \cap(A B C)=A B \\ O H \perp A B \\ S O \perp A B \quad(S O \perp(A B C)) \end{array}\right.\\ &\Rightarrow S H \perp A B \end{aligned}\)
Ta có
\(\begin{aligned} &\left\{\begin{array}{c} (S A B) \cap(A B C)=A B \\ O H \perp A B, O H \subset(A B C) \\ S H \perp A B, S H \subset(S A B) \end{array}\right.\\ &\Rightarrow(\widehat{(S A B) ;(A B C)})=(\widehat{S H ; O H})=\widehat{S H O}=\alpha\\ &\text { Từ (1) suy ra } S H=\sqrt{S A^{2}-A H^{2}}=\sqrt{(2 A B)^{2}-\left(\frac{A B}{2}\right)^{2}}=\frac{\sqrt{15}}{2} A B\\ &\text { Từ đó ta có }: \cos \alpha=\frac{O H}{S H}=\frac{\frac{\sqrt{3}}{6} A B}{\frac{\sqrt{15}}{2} A B}=\frac{1}{3 \sqrt{5}} \end{aligned}\)